题目内容
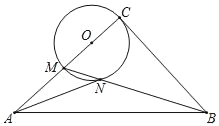
【题目】如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连结BD并延长与CE交于点E．
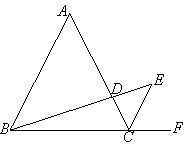
（1）求证：△ABD∽△CED．
（2）若AB＝6，AD＝2CD，求BE的长．
【答案】
（1）略
（2）
【解析】（1）证明：∵ △ABC是等边三角形，
∴ ∠BAC＝∠ACB＝60°．∠ACF＝120°．
∵ CE是外角平分线， ∴ ∠ACE＝60°．
∴ ∠BAC＝∠ACE． ……（2分）
又∵ ∠ADB＝∠CDE，
∴ △ABD∽△CED． ……（4分）
（2）解：作BM⊥AC于点M，AC＝AB＝6．
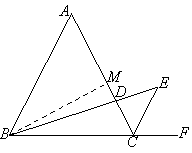
∴ AM＝CM＝3，BM＝AB·sin60°＝
．
∵ AD＝2CD，∴ CD＝2，AD＝4，MD＝1． ……（6分）
在Rt△BDM中，BD＝
＝
． ……（7分）
由（1）△ABD∽△CED得，
，
，
∴ ED＝
，∴ BE＝BD＋ED＝． ……（8分）
练习册系列答案
相关题目
【题目】某班准备选一名学生参加数学史知识竞赛，现统计了两名选手本学期的五次测试 成绩：甲：83，80，90，87， 85； 乙：78，92，82，89，84．
（1）请根据上面的数据完成下表：
极差 | 平均数 | 方差 | |
甲 | 10 | ________ | ________ |
乙 | _________ | 85 | 24.8 |
（2）请你推选出一名参赛选手，并用所学的统计知识说明理由.
