题目内容
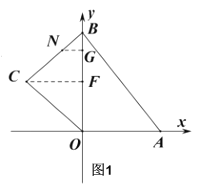
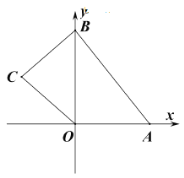
【题目】如图,在平面直角坐标系中,四边形![]() 的顶点
的顶点![]() 是坐标原点,点
是坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() ,
,![]() 分别为四边形
分别为四边形![]() 边上的动点,动点
边上的动点,动点![]() 从点
从点![]() 开始,以每秒1个单位长度的速度沿
开始,以每秒1个单位长度的速度沿![]() 路线向终点
路线向终点![]() 匀速运动,动点
匀速运动,动点![]() 从
从![]() 点开始,以每秒2个单位长度的速度沿
点开始,以每秒2个单位长度的速度沿![]() 路线向终点
路线向终点![]() 匀速运动,点
匀速运动,点![]() 、
、![]() 同时从
同时从![]() 点出发,当其中一点到达终点后,另一点也随之停止运动.设动点运动的时间为
点出发,当其中一点到达终点后,另一点也随之停止运动.设动点运动的时间为![]() 秒(
秒(![]() ),
),![]() 的面积为
的面积为![]() .
.
(1)填空:![]() 的长是________;
的长是________;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)若![]() ,请直接写出此时
,请直接写出此时![]() 的值.
的值.
【答案】(1)6;(2)![]() ;(3)8或
;(3)8或![]() 或
或![]() .
.
【解析】
(1)利用勾股定理即可解决问题;(2)因为OC=6,动点![]() 从
从![]() 点开始,以每秒2个单位长度的速度沿
点开始,以每秒2个单位长度的速度沿![]() 路线向终点
路线向终点![]() 匀速运动,所以当
匀速运动,所以当![]() 时,点N在线段CB上运动,点M在OA上,过
时,点N在线段CB上运动,点M在OA上,过![]() 作
作![]() 轴于点
轴于点![]() ,只要求出OG的值,即为边OM上的高,即可求出结果;(3)当M在OC上时,S最大值=6
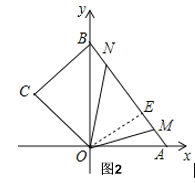
,只要求出OG的值,即为边OM上的高,即可求出结果;(3)当M在OC上时,S最大值=6![]() ,不合题意,然后分三种情形①当点N在边BC上,点M在OA上时.②如图2,当M、N在线段AB上,相遇之前.作OE⊥AB于E,则OE=
,不合题意,然后分三种情形①当点N在边BC上,点M在OA上时.②如图2,当M、N在线段AB上,相遇之前.作OE⊥AB于E,则OE=![]() =
=![]() ,列出方程即可解决问题.③同法当M、N在线段AB上,相遇之后,列出方程即可;
,列出方程即可解决问题.③同法当M、N在线段AB上,相遇之后,列出方程即可;
(1)如图1,作CF⊥OB,B(0,8),C(-2![]() ),∴BF=4,CF=2
),∴BF=4,CF=2![]() ,∴ BC=
,∴ BC=![]() = 6;
= 6;
(2)如,1,当![]() 时,点
时,点![]() 在线段
在线段![]() 上,
上,![]() .过
.过![]() 作
作![]() 轴于点
轴于点![]() ,
,
![]() ,
,![]() ,
,![]() .
.![]() ,
,
![]() ,
,![]() ,
,![]() ,解得
,解得![]() ,
,
![]() ,又∵M(t,0)
,又∵M(t,0)
![]()
(3)8或![]() 或
或![]() .
.
理由:
当M在OC上时,S最大值=![]() ,不合题意;
,不合题意;
然后分三种情况:
①当3<t<6时,由(2)可知![]() ,
,
解得t=![]() (负根已经舍弃).
(负根已经舍弃).
②如图2,当M、N在线段AB上,相遇之前.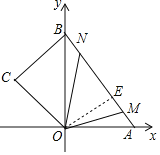
作OE⊥AB于E,易得△AOB∽△AEO,则OE=![]() =
=![]() ,AM=t-6,BN=2t-12,
,AM=t-6,BN=2t-12,
∴![]() [10-(2t-12)-(t-6)]
[10-(2t-12)-(t-6)] ![]() =
=![]() ,解得t=8,
,解得t=8,
③同法当M、N在线段AB上,相遇之后.
由题意可得![]() [(2t-12)+(t-6)-10]
[(2t-12)+(t-6)-10] ![]() =
=![]() ,
,
解得t=![]() ,
,
综上所述,若S=![]() ,此时t的值为8s或
,此时t的值为8s或![]() s或
s或![]() s.
s.