题目内容
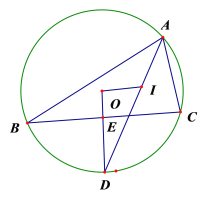
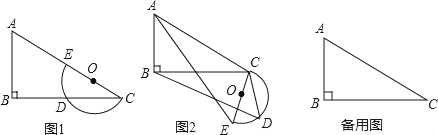
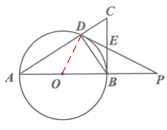
【题目】如图1,在![]() 中,
中,![]() 是
是![]() 的直径,
的直径,![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 的直线交
的直线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,试求
,试求![]() 的长;
的长;
(3)如图2,点![]() 是弧
是弧![]() 的中点,连结
的中点,连结![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.

【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
(1)连接半径![]() ,根据已知条件结合圆的基本性质可推出
,根据已知条件结合圆的基本性质可推出![]() ,即
,即![]() ,即可得证结论;
,即可得证结论;
(2)设![]() ,根据已知条件列出关于
,根据已知条件列出关于![]() 的方程、解方程即可得到圆心角
的方程、解方程即可得到圆心角![]() ,再求得半径,然后利用弧长公式即可得解;
,再求得半径,然后利用弧长公式即可得解;
(3)由![]() ,设
,设![]() ,然后根据已知条件利用圆的一些性质、勾股定理以及三角形的不同求法分别表示出
,然后根据已知条件利用圆的一些性质、勾股定理以及三角形的不同求法分别表示出![]() 、
、![]() ,再利用平行线的判定以及相似三角形的判定和性质即可求得结论.
,再利用平行线的判定以及相似三角形的判定和性质即可求得结论.
解:(1) 连结![]() ,如图:
,如图:
∵![]() 是
是![]() 的直径
的直径
∴![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]() 在圆上
在圆上
∴![]() 是
是![]() 的切线.
的切线.
(2)设![]()
∵![]()
∴![]()
∴![]()
∵在![]() 中,
中,![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
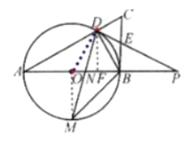
![]() 连结
连结![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,如图:
,如图:
∵点![]() 是
是![]() 的中点
的中点
∴![]()
∴设![]()
∴![]()
∴![]()
∴![]()
∵在![]() 中,
中,![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴ .
.
故答案是:(1)证明见解析(2)![]() (3)
(3)![]()

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
【题目】某品牌手机销售公司有营销员14人,销售部为制定营销人员月销售手机定额,统计了这14人某月的销售量如下(单位:台):
销售量 | 200 | 170 | 165 | 80 | 50 | 40 |
人 数 | 1 | 1 | 2 | 5 | 3 | 2 |
(1)求这14位营销员该月销售该品牌手机的平均数、中位数和众数.
(2)销售部经理把每位营销员月销售量定为100台,你认为是否合理?为什么?