Question

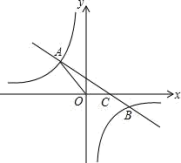
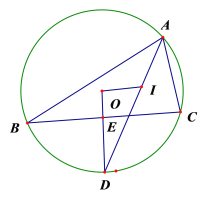
【题目】△ABC内接于⊙O，I为其内心，AI的延长线交⊙O于D,连OD交BC于E．

（1）求证： OD⊥ BC；

（2）若∠BOC=∠BIC，求∠BAC的度数；

（3）①若DE=2,BE=4，①求⊙O的半径r．

②当点A在优弧BAC上移动时，OI是否有最小值，如有请求出最小值，如没有请说明理由．

Answer 1

【答案】（1）见解析；（2）60°（3）①5 ②

【解析】

（1）延长DO交⊙O于P，则DP是⊙O的直径；连接OB、OC，则OB＝OC，根据等边对等角证得∠OBC＝∠OCB，根据内心的性质可得∠∠BAD＝∠CAD，根据圆周角定理及其推论可得∠BOD＝∠BOC，进而证得△BOE≌△COE，继而得BE＝CE，根据垂径定理即可求证结论；

（2）连接BO、CO、BI、CI，根据内心的性质可得∠BIC＝90°＋∠BAC，根据圆周角的性质及其推论可得∠BOC＝2∠BAC，由∠BIC＝∠BOC可知90°＋∠BAC＝2∠BAC，继而求解即可；

（3）①根据题意可得：BE＝4，DE＝2，OB＝r，根据勾股定理列出关于r的方程，解方程即可；

②由I是△ABC的内心可知，DB＝DC＝DI，由勾股定理可得，继而得DI＝DB＝BC＝，分析题意可知，当A点移动到使A、I、O、D四个点在一条直线上时，OI有最小值，继而求得OI＝OD－DI＝5－．

（1）延长DO交⊙O于P，则DP是⊙O的直径；连接OB、OC，则OB＝OC

∴∠OBC＝∠OCB，

∵I是△ABC的内心，

∴AI平分∠BAC，

∴∠BAD＝∠CAD，

∴∠BOD＝∠BOC，

∴△BOE≌△COE（ASA），

∴BE＝CE，

∴DP⊥ BC（平分弦的直径垂直于弦），

即OD⊥ BC，

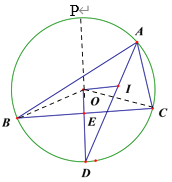
（2）连接BO、CO、BI、CI，

∵I是△ABC的内心，

∴∠BIC＝90°＋∠BAC

∵∠BOC＝2∠BAC，∠BIC＝∠BOC

∴90°＋∠BAC＝2∠BAC，

∴∠BAC＝60°

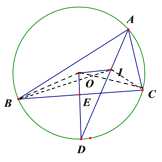
（3）①∵BE＝4，DE＝2，OB＝r

∴OE＝OD－DE＝OB－DE＝r－2，

∵OD⊥BC，

∴∠BEO＝90°，

在Rt△BOE中，根据勾股定理可得

解得：

故⊙O的半径；

②∵⊙O是△ABC的外接圆，I是△ABC的内心，且AI的延长线交⊙O于点D，

∴DB＝DC＝DI，

∵BE＝4，DE＝2，∠BED＝90°,

由勾股定理可得：，

∴DI＝DB＝BC＝,

当A点移动到使A、I、O、D四个点在一条直线上时，OI有最小值，

此时OI＝OD－DI＝5－．