题目内容
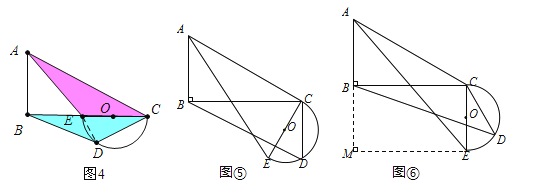
【题目】平面上,Rt△ABC与直径为CE的半圆O如图1摆放,∠B=90°,AC=2CE=m,BC=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转且∠ECD始终等于∠ACB,旋转角记为α(0°≤α≤180°)
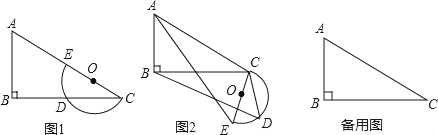
(1)当α=0°时,连接DE,则∠CDE= °,CD= ;
(2)试判断:旋转过程中![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)若m=10,n=8,当α=∠ACB时,求线段BD的长;
(4)若m=6,n=4![]() ,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
【答案】(1)90°,![]() ;(2)无变化;(3)
;(2)无变化;(3)![]() ;(4)BD=
;(4)BD=![]() 或
或![]() .
.
【解析】试题分析:(1)①根据直径的性质,由DE∥AB得![]() 即可解决问题.②求出BD、AE即可解决问题.
即可解决问题.②求出BD、AE即可解决问题.
(2)只要证明△ACE∽△BCD即可.
(3)求出AB、AE,利用△ACE∽△BCD即可解决问题.
(4)分类讨论:①如图5中,当α=90°时,半圆与AC相切,②如图6中,当α=90°+∠ACB时,半圆与BC相切,分别求出BD即可.
试题解析:(1)解:①如图1中,当α=0时,连接DE,则∠CDE=90°.∵∠CDE=∠B=90°,∴DE∥AB,∴![]() =
=![]() .∵BC=n,∴CD=
.∵BC=n,∴CD=![]() .故答案为:90°,
.故答案为:90°,![]() n.
n.
②如图2中,当α=180°时,BD=BC+CD=![]() n,AE=AC+CE=
n,AE=AC+CE=![]() m,∴
m,∴![]() =
=![]() .故答案为:
.故答案为:![]() .
.
(2)如图3中,∵∠ACB=∠DCE,∴∠ACE=∠BCD.∵![]() ,∴△ACE∽△BCD,∴
,∴△ACE∽△BCD,∴![]() .
.
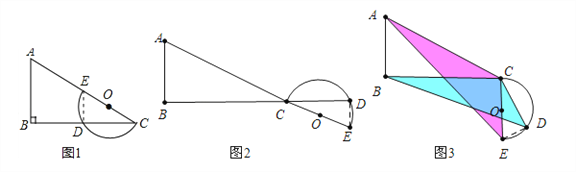
(3)如图4中,当α=∠ACB时.在Rt△ABC中,∵AC=10,BC=8,∴AB=![]() =6.在Rt△ABE中,∵AB=6,BE=BC﹣CE=3,∴AE=
=6.在Rt△ABE中,∵AB=6,BE=BC﹣CE=3,∴AE=![]() =
=![]() =3
=3![]() ,由(2)可知△ACE∽△BCD,∴
,由(2)可知△ACE∽△BCD,∴![]() ,∴
,∴![]() =
=![]() ,∴BD=
,∴BD=![]() .故答案为:
.故答案为:![]() .
.
(4)∵m=6,n=![]() ,∴CE=3,CD=2
,∴CE=3,CD=2![]() ,AB=
,AB=![]() =2,①如图5中,当α=90°时,半圆与AC相切.在Rt△DBC中,BD=
=2,①如图5中,当α=90°时,半圆与AC相切.在Rt△DBC中,BD=![]() =
=![]() =2
=2![]() .
.
②如图6中,当α=90°+∠ACB时,半圆与BC相切,作EM⊥AB于M.∵∠M=∠CBM=∠BCE=90°,∴四边形BCEM是矩形,∴![]() ,∴AM=5,AE=
,∴AM=5,AE=![]() =
=![]() ,由(2)可知
,由(2)可知![]() =
=![]() ,∴BD=
,∴BD=![]() .
.
故答案为:2![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案