题目内容
【题目】如图,等边△ABC中,点D在AC上(CD<![]() AC),连接BD.操作:以A为圆心,AD长为半径画弧,交BD于点E,连接AE.
AC),连接BD.操作:以A为圆心,AD长为半径画弧,交BD于点E,连接AE.
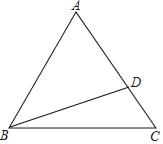
(1)请补全图形,探究∠BAE、∠CBD之间的数量关系,并证明你的结论;
(2)把BD绕点D顺时针旋转60°,交AE于点F,若EF=mAF,求![]() 的值(用含m的式子表示).
的值(用含m的式子表示).
【答案】(1)图形见解析,∠BAE=2∠CBD,理由见解析;(2)![]()
![]() ,理由见解析
,理由见解析
【解析】
(1)根据圆周角和圆心角的关系得:2∠BDH=∠BAE,由等腰三角形的性质得HD∥BC,由平行线的性质可得结论;
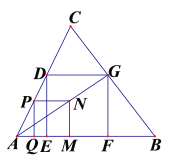
(2)如图2,作辅助线,由旋转得:△BDM是等边三角形,证明△AMB≌△CDB(SAS),得AM=CD,∠MAB=∠C=60°,证明△ABD∽△DFE,设AF=a,列比例式可得结论
(1)如图1,∠BAE=2∠CBD.
设弧DE与AB交于H,连接DH,
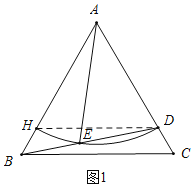
∴2∠BDH=∠BAE,
又∵AD=AH,AB=AC,∠BAC=60°,
∴∠AHD=∠ADH=60°,∠ABC=∠C=60°,
∴∠AHD=∠ABC,
∴HD∥BC,
∴∠DBC=∠HDB,
∴∠BAE=2∠DBC;
(2)如图2,连接AM,BM,
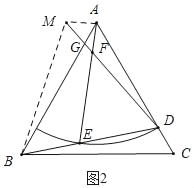
由旋转得:BD=DM,∠BDM=60°,
∴△BDM是等边三角形,
∴BM=BD,∠MBD=60°,
∵∠ABM+∠ABD=∠ABD+∠CBD,
∴∠ABM=∠CBD,
∵△ABC是等边三角形,
∴AB=AC,
∴△AMB≌△CDB(SAS),
∴AM=CD,∠MAB=∠C=60°,
∵∠AGM=∠BGD,∠MAB=∠BDM=60°,
∴∠AMD=∠ABD,
由(1)知:AD=AE,
∴∠AED=∠ADE,
∵∠EDF=∠BAD,
∴△ABD∽△DFE,
∴∠EFD=∠ABD=∠AFM=∠AMD,
∴AF=AM=CD,
设AF=a,则EF=ma,AE=a+ma=(m+1)a,
∴AB=AD+CD=AE+CD=(m+2)a,
由△ABD∽△DFE,
∴![]() =
=![]() =
=![]() .
.

 天天练口算系列答案
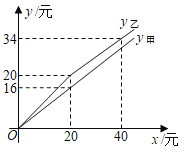
天天练口算系列答案【题目】我市某工艺厂设计了款成本为![]() 元件的工艺品投放市场进行试销,经过调查,得到如下数据:
元件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 | ··· |
|
|
|
| ··· |
每天销售量 | ··· |
|
|
|
| ··· |
(1)若![]() 是
是![]() 的一次函数,求出此函数的关系式:
的一次函数,求出此函数的关系式:
(2)若用![]() (元)表示工艺厂试销该工艺品每天获得的利润,试求
(元)表示工艺厂试销该工艺品每天获得的利润,试求![]() (元)与
(元)与![]() (元/件)之间的函数关系式.
(元/件)之间的函数关系式.
(3)若该工艺品的每天的总成木不能超过![]() 元,那么销售单价定为多少元时,工艺厂试销工艺品每天获得的利润最大,最大是多少元?
元,那么销售单价定为多少元时,工艺厂试销工艺品每天获得的利润最大,最大是多少元?