Question

【题目】如图，在△ABC中，∠ACB＝90°，AC＝6，BC＝12，动点M从A点出发，以每秒1个单位长度的速度沿着AC方向向C点运动，动点N从C点出发，以每秒2个单位长度的速度沿着CB方向向B点运动，如果M，N两点同时出发，当M到达C点处时，两点都停止运动，设运动的时间为t秒，四边形AMNB的面积为S．

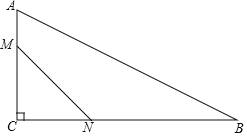
（1）用含t的代数式表示：CM＝　 　，CN＝　 　．

（2）当t为何值时，△CMN与△ABC相似？

（3）求S和t的关系式（写出自变量t的取值范围）；当t取何值时，S的最小，并求最小值．

Answer 1

【答案】（1）CM＝6﹣t，CN＝2t；（2）t为3或1.2；（3）（t-3）2+27（0＜t＜6），t＝3，27

【解析】

（1）先由运动得出AM＝t，CN＝2t，继而得出CM，即可得出结论；

（2）分两种情况，利用相似三角形得出的比例式建立方程求解，即可得出结论；

（3）利用三角形的面积的差即可得出结论．

解：（1）由运动知，AM＝t，CN＝2t，

∵AC＝6，

∴CM＝AC﹣AM＝6﹣t，

故答案为：6﹣t，2t；

（2）由（1）知，CM＝6﹣t，CN＝2t，

①当△CMN∽△CAB时，

∴，

∵AC＝6，BC＝12，

∴，

∴t＝3，

②当△CMN∽△CBA，

∴，

∴，

∴t＝1.2，

即：t为3或1.2时，△CMN与△ABC相似；

（3）由（1）知，CM＝6﹣t，CN＝2t，

∴S四边形AMNB＝S△ABC﹣S△CMN＝×6×12﹣×2t×（6﹣t）＝（t-3）2+27（0＜t＜6），

当t＝3时，S四边形AMNB最小＝27