Question

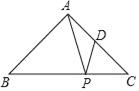
【题目】已知：如图，ABCD的对角线AC、BD相交于点O，∠BDC＝45°，过点B作BH⊥DC交DC的延长线于点H，在DC上取DE＝CH，延长BH至F，使FH＝CH，连接DF、EF．

（1）若AB＝2，AD＝，求BH的值；

（2）求证：AC＝EF．

Answer 1

【答案】（1）3；（2）见解析

【解析】

（1）过点A作AN⊥BD于N，证出△ABN是等腰直角三角形，得出AN＝BN＝AB＝，DN＝2，得出BD＝BN+DN＝+2＝3，证出△BDH是等腰直角三角形，即可得出BH＝DH＝BD＝3；

（2）取DH的中点M，连接OM，证出OM是△BDH的中位线，得出OM∥BH，OM＝BH＝DH＝DM，设DE＝a，CE＝b，则CH＝FH＝a，CD＝EH＝CE+CH＝a+b，BH＝DH＝DE+CE+CH＝2a+b，得出OM＝DM＝（2a+b），CM＝CD﹣DM＝b，在Rt△OMC中，由勾股定理得出OC2＝（2a+b）2+b2＝AC2，得出AC2＝（2a+b）2+b2＝4a2+4ab+2b2＝2（2a2+2ab+b2），在Rt△EHF中，由勾股定理得出EF2＝2a2+2ab+b2，得出AC2＝2EF2，即可得出结论．

（1）解：过点A作AN⊥BD于N，如图1所示：

∵四边形ABCD为平行四边形，

∴AB∥CD，

∴∠ABD＝∠BDC＝45°，

∵AN⊥BD，

∴△ABN是等腰直角三角形，

∵AB＝2，

∴AN＝BN＝AB＝，DN＝＝＝2，

∴BD＝BN+DN＝+2＝3，

∵BH⊥DC，

∴△BDH是等腰直角三角形，

∴BH＝DH＝BD＝×3＝3；

（2）证明：取DH的中点M，连接OM，如图2所示：

∵四边形ABCD是平行四边形，

∴OB＝OD，

∴OM是△BDH的中位线，

∴OM∥BH，OM＝BH＝DH＝DM，

设DE＝a，CE＝b，则CH＝FH＝a，CD＝EH＝CE+CH＝a+b，BH＝DH＝DE+CE+CH＝2a+b，

∴OM＝DM＝（2a+b），

∴CM＝CD﹣DM＝a+b﹣（2a+b）＝b，

在Rt△OMC中，由勾股定理得：OC2＝OM2+CM2＝（2a+b）2+b2＝AC2，

∴AC2＝（2a+b）2+b2＝4a2+4ab+2b2＝2（2a2+2ab+b2），

在Rt△EHF中，由勾股定理得：EF2＝EH2+FH2＝（a+b）2+a2＝2a2+2ab+b2，

∴AC2＝2EF2，

∴AC＝EF．