题目内容
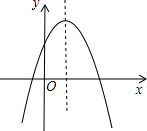
请画出函数y=-
x2+x-
的图象,并说明这个函数具有哪些性质.
| 1 |
| 2 |
| 5 |
| 2 |
(1)列表:在x的取值范围内列出函数对应值表;
(2)描点:用表格里各组对应值作为点的坐标,在平面直角坐标系中描点.
(3)连线:用光滑的曲线顺次连接各点,得到函数y=-
x2+x-
的图象.
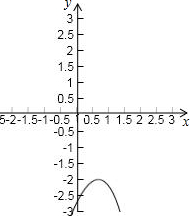
则可得到这个函数的性质如下:
当x<1时,函数值y随x的增大而增大;当x>1时,函数值y随x的增大而减小;
当x=1时,函数取得最大值,最大值y=-2.
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … | ||||||||
| y | … | -6
| -4 | -2
| -2 | -2
| -4 | -6
| … |
(3)连线:用光滑的曲线顺次连接各点,得到函数y=-
| 1 |
| 2 |
| 5 |
| 2 |
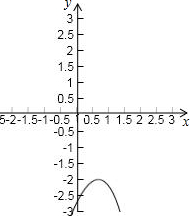
则可得到这个函数的性质如下:
当x<1时,函数值y随x的增大而增大;当x>1时,函数值y随x的增大而减小;
当x=1时,函数取得最大值,最大值y=-2.

练习册系列答案
相关题目
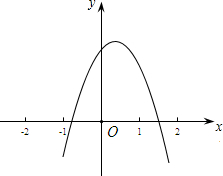
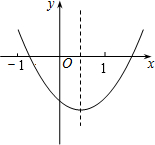

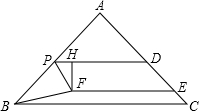 AP=x.
AP=x.