题目内容
已知点A(a,y1)、B(2a,y2)、C(3a,y3)都在抛物线y=5x2+12x上.
(1)求抛物线与x轴的交点坐标;
(2)当a=1时,求△ABC的面积.
(1)求抛物线与x轴的交点坐标;
(2)当a=1时,求△ABC的面积.
(1)根据题意,令y=0,即5x2+12x=0,得x1=0,x2=-
,
∴抛物线与x轴的交点坐标为(0,0)、(-
,0).
(2)当a=1时,可把A、B、C代入解析式,
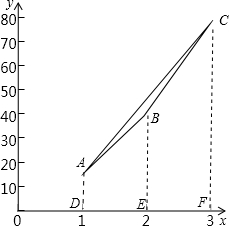
得A(1,17)、B(2,44)、C(3,81),
分别过点A、B、C作x轴的垂线,垂足分别为D、E、F,如图:
则有S△ABC=S梯形ADFC-S梯形ADEB-S梯形EBFC
=
-
-
=5.
| 12 |
| 5 |
∴抛物线与x轴的交点坐标为(0,0)、(-
| 12 |
| 5 |
(2)当a=1时,可把A、B、C代入解析式,
得A(1,17)、B(2,44)、C(3,81),
分别过点A、B、C作x轴的垂线,垂足分别为D、E、F,如图:
则有S△ABC=S梯形ADFC-S梯形ADEB-S梯形EBFC
=
| (17+81)×2 |
| 2 |
| (17+44)×1 |
| 2 |
| (44+81)×1 |
| 2 |


练习册系列答案
相关题目