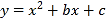题目内容
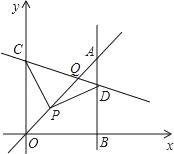
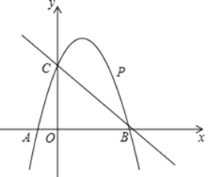
【题目】如图,已知二次函数y=ax2+bx+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0),AB=4.
(1)求二次函数y=ax2+bx+c的表达式;
(2)点M是二次函数对称轴上一动点,当点M运动到什么位置时,△ACM的周长最小?求出此时M点的坐标;
(3)点P是直线BC上方的抛物线上一动点,当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
【答案】(1)y=﹣x2+2x+3(2)(1,2)(3)当点P的坐标为(![]() ,
,![]() )时,四边形ACPB的最大面积值为
)时,四边形ACPB的最大面积值为![]()
【解析】
(1)根据待定系数法,可得函数解析式;
(2)要使△ACM的周长最小,AC长不变,即为AM+CM的和最小, 点A、点B关于对称轴对称,所以点M为对称轴与直线BC的交点;
(3)根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PQ的长,根据面积的和差,可得二次函数,根据二次函数的性质,可得答案.
(1)因为AB=4,所以A点的坐标(-1,0),
将点A、点B和点C的坐标代入函数解析式,得
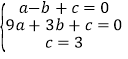 ,解得
,解得
二次函数的解析式为y=﹣x2+2x+3;
(2)对称轴x=1,要使△ACM的周长最小,AC长不变,即为AM+CM的和最小.
点A、点B关于对称轴对称,所以点M为对称轴与直线BC的交点.
设直线BC的解析式为y=kx+t,
将点B和点C的坐标代入函数解析式,得![]()
解得![]()
直线BC的解析为y=﹣x+3,
当x=1时,y=2.则M(1,2)
(3)如图2,过点P,PF⊥x轴,交CB于点Q
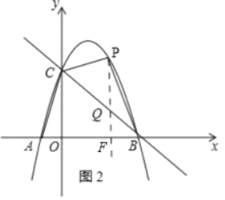
P在抛物线上,设P(m,﹣m2+2m+3),
直线BC的解析为y=﹣x+3,
设点Q的坐标为(m,﹣m+3),
PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m.
AB=4,
S四边形ABPC=S△ABC+S△PCQ+S△PBQ
=![]() ABOC+
ABOC+![]() PQOF+
PQOF+![]() PQFB
PQFB
=![]() ×4×3+
×4×3+![]() (-m2+3m)×3
(-m2+3m)×3
=-![]() (m-
(m-![]() )2+
)2+![]() ,
,
当m=![]() 时,四边形ABPC的面积最大.
时,四边形ABPC的面积最大.
当m=![]() 时,-m2+2m+3=
时,-m2+2m+3=![]() ,即P点的坐标为(
,即P点的坐标为(![]() ,
,![]() ).
).
当点P的坐标为(![]() ,
,![]() )时,四边形ACPB的最大面积值为
)时,四边形ACPB的最大面积值为![]() .
.