题目内容
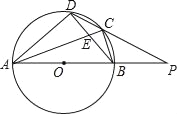
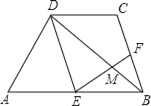
【题目】如图,AB∥CD,且AB=2CD,E是AB的中点,F是边BC上的动点,EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若F是BC的中点,BD=12,求BM的长;
(3)若AD=BC,BD平分∠ABC,点P是线段BD上的动点,是否存在点P使DPBP=BFCD,若存在,求出∠CPF的度数;若不存在,请说明理由.
【答案】(1)证明见解析;(2)BM=4;(3)存在,∠CPF=30°.
【解析】
(1)根据题意及中点的性质得出四边形CBED是平行四边形,根据平行的性质得出∠EDB=∠FBM,∠DME=∠BMF,从而得出△EDM∽△FBM;
(2)根据(1)中三角形相似的比例关系即可推理得出答案;
(3)先由角平分线的定义和平行线的性质可得DC=BC,结合DPBP=BFCD可证明△PDC∽△FBP,从而∠BPF=∠PCD,利用三角形内角和及平角定义可证∠PDC=∠CPF,然后通过证明△ADE是等边三角形,可进一步求出结论.
(1)证明:∵AB=2CD,点E是AB的中点,
∴DC=EB.
又∵AB∥CD,
∴四边形BCDE为平行四边形.
∴ED∥BC.
∴∠EDB=∠FBM.
又∵∠DME=∠BMF,
∴△EDM∽△FBM;
(2)解:∵△EDM∽△FBM,
∴![]() ,
,
∵F是BC的中点,
∴DE=BC=2BF,
∴DM=2BM,
∴DB=DM+BM=3BM,
∵DB=12,
∴BM=![]() DB=
DB=![]() ×12=4;
×12=4;
(3)存在,∵DC∥AB,
∴∠CDB=∠ABD,
∵BD平分∠ABC,
∴∠CBD=∠ABD,
∴∠CDB=∠CBD,
∴DC=BC,
∵DPBP=BFCD,
∴![]() ,
,
∴△PDC∽△FBP,
∴∠BPF=∠PCD,
∵∠DPC+∠CPF+∠BPF=180°,
∠DPC+∠PDC+∠PCD=180°,
∴∠PDC=∠CPF,
∵AD=BC=DC=BE=AE,
∴△ADE是等边三角形,
∴∠AED=60°,
∴∠EDB=∠PDC=30°,
∴∠CPF=30°.


【题目】某小区改善生态环境,实行生活垃圾的分类处理,将生活垃圾分成三类:厨房垃圾、可回收垃圾和其他垃圾,分别记为m,n,p,并且设置了相应的垃圾箱,“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率;
(2)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共1 000吨生活垃圾,数据统计如下(单位:吨):
A | B | C | |
m | 400 | 100 | 100 |
n | 30 | 240 | 30 |
p | 20 | 20 | 60 |
请根据以上信息,试估计“厨房垃圾”投放正确的概率.