题目内容
【题目】抛物线![]() 与
与![]() 轴交于A、B两点,点P在函数
轴交于A、B两点,点P在函数![]() 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
A. 2个 B. 3个 C. 4个 D. 6个
【答案】D
【解析】分析:先由二次函数与一元二次方程的关系求出A、B两点的坐标,然后分类讨论:①当∠PAB=90°时,则P点的横坐标为-3,根据反比例函数图象上点的坐标特征易得P点有1个;②当∠APB=90°,设P(x,![]() ),根据两点间的距离公式和勾股定理可得(x+3)2+(
),根据两点间的距离公式和勾股定理可得(x+3)2+(![]() )2+(x-3)2+(
)2+(x-3)2+(![]() )2=36,此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,此时P点有1个.
)2=36,此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,此时P点有1个.
详解:解![]() 得,
得,
x=±3,
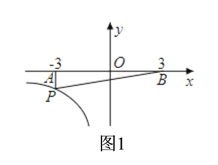
∴A(-3,0),B(3,0).
①当∠PAB=90°时,如图1,P点的横坐标为-3,把x=-3代入y=![]() 得y=-
得y=-![]() ,所以此时P点有1个;
,所以此时P点有1个;
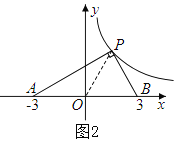
②当∠APB=90°,如图2,设P(x,![]() ),PA2=(x+3)2+(
),PA2=(x+3)2+(![]() )2,PB2=(x-3)2+(
)2,PB2=(x-3)2+(![]() )2,AB2=(3+3)2=36,
)2,AB2=(3+3)2=36,
∵PA2+PB2=AB2,
∴(x+3)2+(![]() )2+(x-3)2+(
)2+(x-3)2+(![]() )2=36,
)2=36,
整理得x4-9x2+4=0,所以x2=![]() ,或x2=
,或x2=![]() ,
,
所以此时P点有4个,
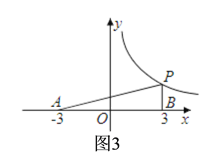
③当∠PBA=90°时,如图3,P点的横坐标为3,把x=3代入y=![]() 得y=
得y=![]() ,所以此时P点有1个;
,所以此时P点有1个;
综上所述,满足条件的P点有6个.
故选:D.

练习册系列答案
相关题目