Question

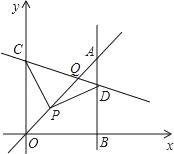
【题目】如图，平面直角坐标系中，已知P（1，1），C为y轴正半轴上一点，D为第一象限内一点，且PC＝PD，∠CPD＝90°，过点D作直线AB⊥x轴于B，直线AB与直线y＝x交于点A，且BD＝3AD，连接CD，直线CD与直线y＝x交于点Q，则点Q的坐标为_____．

Answer 1

【答案】(，)

【解析】

过P作MN⊥y轴，交y轴于M，交AB于N，过D作DH⊥y轴，交y轴于H，∠CMP=∠DNP=∠CPD=90°，求出∠MCP=∠DPN，证△MCP≌△NPD，推出DN=PM，PN=CM，设AD=a，求出DN=3a-1，得出3a-1=1，求出a=，得出D的坐标，在Rt△DNP中，由勾股定理求出PC=PD=，在Rt△MCP中，由勾股定理求出CM，得出C的坐标，设直线CD的解析式是y=kx+，把D（，2）代入求出直线CD的解析式，解由两函数解析式组成的方程组，求出方程组的解即可．

过P作MN⊥y轴，交y轴于M，交AB于N，过D作DH⊥y轴，交y轴于H，

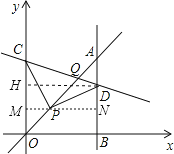
则∠CMP=∠DNP=∠CPD=90°，

∴∠MCP+∠CPM=90°，∠MPC+∠DPN=90°，

∴∠MCP=∠DPN，

∵P（1，1），

∴OM=BN=1，PM=1，

在△MCP和△NPD中，

，

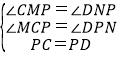∴△MCP≌△NPD（AAS），

∴DN=PM，PN=CM，

∵BD=3AD，

∴设AD=a，BD=3a，

∵P（1，1），

∴DN=3a-1，

则3a-1=1，

∴a=，即BD=2，

∵点A在直线y=x上，

∴AB=OB=，

在Rt△DNP中，由勾股定理得：PC=PD==，

在Rt△MCP中，由勾股定理得：CM==，

则C的坐标是（0，），

设直线CD的解析式是y=kx+，

把D（，2）代入得：k=-，

即直线CD的解析式是y=-x+，

解方程组，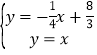

得：，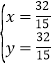

即Q的坐标是（，），

故答案为：（，）．