题目内容
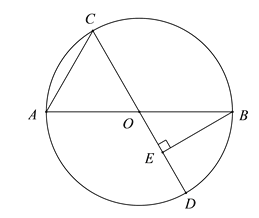
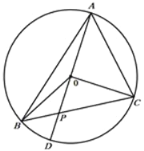
【题目】如图,△ABC内接于圆O,∠BOC=120°,AD为圆O的直径.AD交BC于P点且PB=1,PC=2,则AC的长为( )
A. ![]() B.
B. ![]() C. 3D. 2
C. 3D. 2![]()
【答案】A
【解析】
延长CO交⊙O于E,连接BE,由CE是⊙O的直径,推出∠EBC=90°,根据含30°直角三角形定理可求得BC,CE,进而求得OA=OD=![]() ,通过计算证得
,通过计算证得![]() ,由相似三角形的判定证得△OCP∽△BCE,即可证得∠POC=∠PBE=90°,根据勾股定理即可求得结论.
,由相似三角形的判定证得△OCP∽△BCE,即可证得∠POC=∠PBE=90°,根据勾股定理即可求得结论.
延长CO交⊙O于E,连接BE,
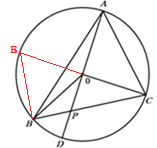
∵CE是⊙O的直径,
∴∠EBC=90°,
∵∠BOC=120°
∴∠BAC=![]() ∠BOC=60°
∠BOC=60°
∴∠BEC=∠BAC=60°,
∴∠ECB=30°,
∴CE=2BE,
∵PB=1,PC=2,
则BC=3,
![]() ,
,
∴CE=![]() ,
,
则OA=OD=![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
又∵∠OCP=∠BCE,
∴△OCP∽△BCE,
∴∠POC=∠PBE=90°,
∴AD2=OA2+OC2=6,
∴AD=![]() .
.
故选A.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
【题目】我市部分学生参加了全国初中数学竞赛决赛,并取得优异成绩.已知竞赛成绩分数都是整数,试题满分为140分,参赛学生的成绩分数分布情况如下:
分数段 | 0-19 | 20-39 | 40-59 | 60-79 | 80-99 | 100-119 | 120-140 |
人数 | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
请根据以上信息解答下列问题:
(1)全市共有多少人参加本次数学竞赛决赛?最低分和最高分在什么分数范围?
(2)经竞赛组委会评定,竞赛成绩在60分以上(含60分)的考生均可获得不同等级的奖励,求我市参加本次竞赛决赛考生的获奖比例;
(3)决赛成绩分数的中位数落在哪个分数段内?
(4)上表还提供了其他信息,例如:“没获奖的人数为105人”等等.请你再写出两条此表提供的信息.