题目内容
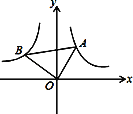
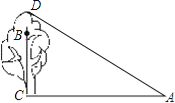
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知
与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知![]() ,
,![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
![]() 点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,
点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,![]() 的面积最大?求出
的面积最大?求出![]() 的最大面积及此时E点的坐标.
的最大面积及此时E点的坐标.

【答案】(1)![]() ;(2)存在,P点的坐标为
;(2)存在,P点的坐标为![]() 或
或![]() 或
或![]() :(3)当E运动到BC的中点时,
:(3)当E运动到BC的中点时,![]() 面积最大为
面积最大为![]() ,此时
,此时![]() .
.
【解析】
![]() 把
把![]() ,
,![]() 代入
代入![]() 列方程组即可.
列方程组即可.
![]() 先求出CD的长,分两种情形
先求出CD的长,分两种情形![]() 当
当![]() 时,
时,![]() 当
当![]() 时分别求解即可.
时分别求解即可.
![]() 求出直线BC的解析式,设
求出直线BC的解析式,设![]() 则
则![]() ,构建二次函数,利用二次函数的性质即可解决问题.
,构建二次函数,利用二次函数的性质即可解决问题.
解:![]() 把
把![]() ,
,![]() 代入
代入![]() 得
得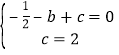 ,
,
解得![]() ,
,![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
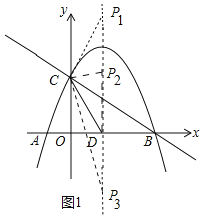
![]() 存在
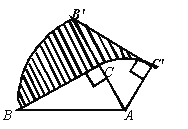
存在![]() 如图1中,
如图1中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
![]() 当
当![]() 时,可得
时,可得![]() .
.
![]() 当
当![]() 时,可得
时,可得![]() ,
,![]()
综上所述,满足条件的P点的坐标为![]() 或
或![]() 或
或![]() .
.
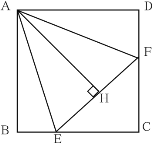
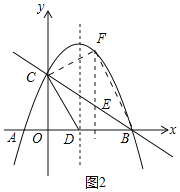
![]() 如图2中,
如图2中,
对于抛物线![]() ,当
,当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]()
![]() ,
,![]() ,
,
由![]() ,
,![]() 得直线BC的解析式为
得直线BC的解析式为![]() ,
,
设![]() 则
则![]() ,
,
![]()
![]() ,
,![]() 当
当![]() 时,EF有最大值2,
时,EF有最大值2,
此时E是BC中点,
![]() 当E运动到BC的中点时,
当E运动到BC的中点时,![]() 面积最大,
面积最大,
![]() 最大面积
最大面积![]() ,此时
,此时![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
【题目】某公司改革实行每月考核再奖励的新制度,大大调动了员工的积极性,![]() 年一名员工每月奖金的变化如下表:(正数表示比前一月多的钱数,负数表示比前一月少的钱数)单位:(元)
年一名员工每月奖金的变化如下表:(正数表示比前一月多的钱数,负数表示比前一月少的钱数)单位:(元)
月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
钱数变化 |
|
|
|
|
|
|
|
(1)若![]() 年底
年底![]() 月份奖金为
月份奖金为![]() 元,用代数式表示
元,用代数式表示![]() 年二月的奖金;
年二月的奖金;
(2)请判断七个月以来这名员工得到奖金最多是哪个月?最少是哪个月?他们相差多少元?
(3)若![]() 年这七个月中这名员工最多得到的奖金是
年这七个月中这名员工最多得到的奖金是![]() 元,请问
元,请问![]() 年
年![]() 月份他得到多少奖金?
月份他得到多少奖金?