Question

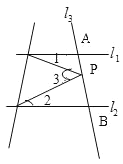
【题目】如图,已知直线11∥12,且13和11、12分别交于A、B两点,点P在直线AB上.

(1)试猜想写出∠1,∠2,∠3之间的关系式，并加以证明.

(2)如果点P在A、B两点外侧(点P和A、B不重合)运动时,试画出图形，写出∠1,∠2,∠3之间的关系，并加以证明.

Answer 1

【答案】(1)∠1+∠2=∠3，证明见解析；(2)∠1+∠3=∠2或∠2+∠3=∠1，证明见解析.

【解析】

（1）过点P作l1的平行线，依据平行线的性质可得∠1=∠CPQ，∠2=∠DPQ，根据∠CPQ+∠DPQ=∠3，即可得到∠1+∠2=∠3；

（2）当点P在下侧时，过点P作l1的平行线PQ，依据平行线的性质可得∠1-∠2=∠3；当点P在上侧时，同理可得：∠2-∠1=∠3．

解：（1）∠1+∠2=∠3；
理由：如图，过点P作l1的平行线，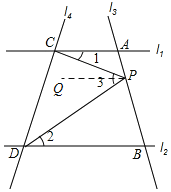

∵l1∥l2，
∴l1∥l2∥PQ，
∴∠1=∠CPQ，∠2=∠DPQ，
∵∠CPQ+∠DPQ=∠3，
∴∠1+∠2=∠3；

（2）∠1-∠2=∠3或∠2-∠1=∠3；
理由：当点P在下侧时，过点P作l1的平行线PQ，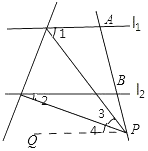

∵l1∥l2，
∴l1∥l2∥PQ，
∴∠2=∠4，∠1=∠3+∠4，（两直线平行，内错角相等）
∴∠1-∠2=∠3；
当点P在上侧时，同理可得：∠2-∠1=∠3．