题目内容
【题目】完成下面的证明过程：
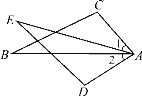
如图所示，直线AD与AB，CD分别相交于点A，D，与EC，BF分别相交于点H，G，已知∠1＝∠2，∠B＝∠C．
求证：∠A＝∠D．
证明：∵∠1＝∠2，（已知）∠2＝∠AGB（ ）
∴∠1＝ （ ）
∴EC∥BF（ ）
∴∠B＝∠AEC（ ）
又∵∠B＝∠C（已知）
∴∠AEC＝ （ ）
∴ （ ）
∴∠A＝∠D（ ）
【答案】见解析
【解析】
根据平行线的性质与判定即可写出.
证明：∵∠1＝∠2（已知），∠2＝∠AGB（对顶角相等）
∴∠1＝∠AGB
∴EC∥BF（同位角相等，两直线平行）
∴∠B＝∠AEC（两直线平行，同位角相等）
又∵∠B＝∠C（已知）
∴∠AEC＝ ∠C （等量替换）
∴AB∥CD（内错角相等，两直线平行）
∴∠A＝∠D（两直线平行，内错角相等）
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】为了加强公民节水意识，合理利用水资源，某市采用价格调控手段达到节约用水的目的，规定：每户居民每月用水不超过15m3时，按基本价格收费；超过15m3时，不超过的部分仍按基本价格收费，超过的部分要加价收费，该市某户居民今年4、5月份的用水量和水费如表所示：
月份 | 用水量/m3 | 水费/元 |
4 | 16 | 50 |
5 | 20 | 70 |
（1）求该市居民用水的两种收费价格；
（2）若该居民6月份交水费80元，那么该居民这个月水量为m3 ．
