题目内容
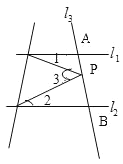
【题目】如图：在四边形ABCD中，AD∥BC，且BC=12cm，AD=18cm，P、Q分别从A、C同时出发，P以2cm/s的速度由A向D运动，Q以4cm/s的速度由C向B运动，问当多少秒时,直线QP将四边形ABCD截出一个平行四边形．
【答案】2或3秒
【解析】
此题应分两种情况讨论：①构成的是平行四边形APQB，此时BQ=AP，②构成的是平行四边形CQPD，此时CQ=PD；用时间t表示出CQ、BQ、AP、PD的长，然后根据上面的等量关系求得t的值．
设点P、Q运动的时间为t秒，依题意有：CQ=4t， BQ=12-4t，AP=2t， PD=18-2t；
∵AD∥BC，
∴①当BQ=AP时，四边形APQB是平行四边形，
即12-4t=2t，
解得t=2；
②当CQ=PD时，四边形CQPD是平行四边形，
即4t=18-2t，
解得t=3；
所以当2或3秒时，直线QP将四边形截出一个平行四边形．
寒假学与练系列答案
【题目】对某市中学生的幸福指数进行调查，从中抽取部分学生的调查表问卷进行统计，并绘制出不完整的统计表和条形统计图。
等级 | 频数 | 频率 |
★ | 60 | |
★★ | 80 | |
★★★ | 0.16 | |
★★★★ | 0.30 | |
★★★★★ |
（1）直接补全统计表；
（2）补全条形统计图（不要求写出计算过程）；
（3）抽查的学生约占全市中学生的5%，估计全市约有多少名学生的幸福指数能达到五★级？
【题目】近年来，我国很多地区持续出现雾霾天气．某社区为了调查本社区居民对雾霾天气主要成因的认识情况，随机对该社区部分居民进行了问卷调查，要求居民从五个主要成因中只选择其中的一项，被调查居民都按要求填写了问卷．社区对调查结果进行了整理，绘制了如下不完整的统计图表．被调查居民选择各选项人数统计表
雾霾天气的主要成因 | 频数（人数） |
A大气气压低，空气不流动 | m |
B地面灰尘大，空气湿度低 | 40 |
C汽车尾气排放 | n |
D工厂造成的污染 | 120 |
E其他 | 60 |
请根据图表中提供的信息解答下列问题：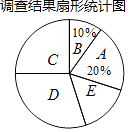
（1）填空：m= ， n= ， 扇形统计图中C选项所占的百分比为 ．
（2）若该社区居民约有6 000人，请估计其中会选择D选项的居民人数．
（3）对于“雾霾”这个环境问题，请你用简短的语言发出倡议．