题目内容
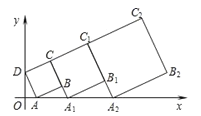
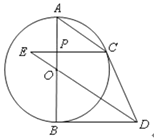
【题目】如图,AB是⊙O的直径,DB切⊙O于点B,C是圆上一点,过点C作AB的垂线,交AB于点P,与DO的延长线交与点E,且ED∥AC,连接CD.
(1)求证:CD是⊙O的切线;
(2)若AB=12,OP:AP=1:2,求ED的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OC,根据切线的性质可得∠OBD=90°,然后利用SAS证出![]() ≌
≌![]() ,可得∠OCD=∠OBD=90°,从而证出结论;
,可得∠OCD=∠OBD=90°,从而证出结论;
(2)根据圆的直径和线段比,求出OB、OA、OC、OP和AP,证出![]() ∽
∽![]() ,列出比例式即可求出EO,再证出
,列出比例式即可求出EO,再证出![]() ∽
∽![]() ,列出比例式即可求出OD,从而求出结论.
,列出比例式即可求出OD,从而求出结论.
(1)证明:连接OC.
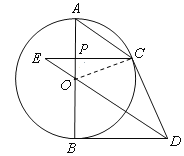
∵DB切⊙O于点B,
∴∠OBD=90°.
∵OA=OC,
∴∠ACO=∠CAO.
∵OD∥AC,
∴∠COD=∠ACO,∠CAO=∠BOD,
∴∠COD=∠BOD.
又∵OC=OB,OD=OD,
∴![]() ≌
≌![]() (SAS),
(SAS),
∴∠OCD=∠OBD=90°,即CD是⊙O的切线.
(2)解:∵AB=12,AB是直径,
∴OB=OA=6.
∵OP∶AP=1∶2,
∴OP=2,AP=4.
∵∠APC=90°,OC=6,
∴PC=![]() ,AC=
,AC=![]() .
.
∵ED∥AC,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
即![]() ,
,
解得![]() .
.
∵∠EPO=∠B=90°,∠EOP=∠DOB
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴ED=EO+OD=![]() .
.

【题目】经过举国上下抗击新型冠状病毒的斗争,疫情得到了有效控制,国内各大企业在2月9日后纷纷进入复工状态.为了了解全国企业整体的复工情况,我们查找了截止到2020年3月1日全国部分省份的复工率,并对数据进行整理、描述和分析.下面给出了一些信息:
a.截止3月1日20时,全国已有11个省份工业企业复工率在90%以上,主要位于东南沿海地区,位居前三的分别是贵州(100%)、浙江(99.8%)、江苏(99%).
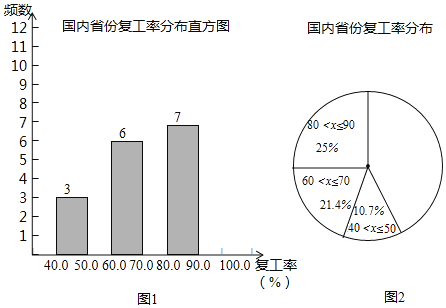
b.各省份复工率数据的频数分布直方图如图1(数据分成6组,分别是40<x≤50;
50<x≤60;60<x≤70;70<x≤80;80<x≤90;90<x≤100):
c.如图2,在b的基础上,画出扇形统计图:
d.截止到2020年3月1日各省份的复工率在80<x≤90这一组的数据是:
81.3 | 83.9 | 84 | 87.6 | 89.4 | 90 | 90 |
e.截止到2020年3月1日各省份的复工率的平均数、中位数、众数如下:
日期 | 平均数 | 中位数 | 众数 |
截止到2020年3月1日 | 80.79 | m | 50,90 |
请解答以下问题:
(1)依据题意,补全频数分布直方图;
(2)扇形统计图中50<x≤60这组的圆心角度数是 度(精确到0.1).
(3)中位数m的值是 .
(4)根据以上统计图表简述国内企业截止3月1日的复工率分布特征.