题目内容
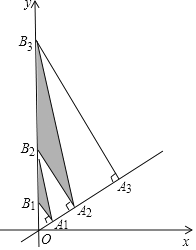
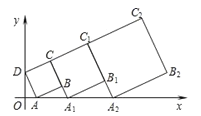
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2020个正方形的面积是____.
【答案】![]()
【解析】
先利用勾股定理求出AB=BC=AD,再用三角形相似得出A1B=![]() ,A2B2=
,A2B2=![]() ,找出规律A2020B2020=
,找出规律A2020B2020=![]() ,即可.
,即可.
解:∵点A的坐标为(1,0),点D的坐标为(0,2),
∴OA=1,OD=2,BC=AB=AD=![]() ,
,
∵正方形ABCD,正方形A1B1C1C,
∴∠OAD+∠A1AB=90°,∠ADO+∠OAD=90°,
∴∠A1AB=∠ADO,
∵∠AOD=∠A1BA=90°,
∴△AOD∽△A1BA,
∴![]() ,即
,即![]()
∴A1B=![]() ,
,
∴A1B1=A1C=A1B+BC=![]() ,
,
同理可得,A2B2=![]() =
=![]() ,
,
同理可得,A3B3=![]() ,
,
同理可得,A2020B2020=![]() ,
,
∴第2020个正方形的面积=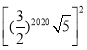 =
=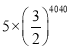
故答案为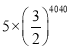 .
.

练习册系列答案
相关题目