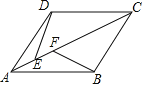
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩάœ ΠΥφΜζ≥ι≤ιΝΥ±Ψ―ßΤΎ―ß…ζ‘ΡΕΝΩΈΆβ ι≤α ΐΒΡ«ιΩωΘ§≤ΔΫΪ≥ι≤ιΫαΙϊΜφ÷Τ≥…Χθ–ΈΆΦΘ®ΆΦ1Θ©ΚΆ≤ΜΆξ’ϊΒΡ…»–ΈΆΦΘ®ΆΦ2Θ©Θ§Τδ÷–Χθ–ΈΆΦ±ΜΡΪΦΘ’ΎΗ«ΝΥ“Μ≤ΩΖ÷Θ°

Θ®1Θ©Χθ–ΈΆΦ÷–±Μ’ΎΗ«ΒΡ»Υ ΐΈΣΓΓ ΓΓΘ§±Μ≥ι•ΥΒΡ―ß…ζΕΝ ι≤α ΐΒΡ÷–ΈΜ ΐΈΣΓΓ ΓΓΘ°
Θ®2Θ©…»–ΈΆΦ÷–5≤αΥυ’ΦΒΡ‘≤–ΡΫ«ΒΡΕ» ΐΈΣΓΓ ΓΓΘΜ
Θ®3Θ©‘ΎΥυ≥ι≤ιΒΡ―ß…ζ÷–ΥφΜζ―Γ“Μ»ΥΧΗΕΝ ιΗ–œκΘ§«σ―Γ÷–ΕΝ ι≥§Ιΐ5≤αΒΡ―ß…ζΒΡΗ≈¬ ΘΜ
Θ®4Θ©ΥφΚσ”÷≤Ι≤ιΝΥΝμΆβΦΗ»ΥΘ§ΒΟ÷ΣΉν…ΌΒΡΕΝΝΥ6≤αΘ§ΫΪ≤Ι≤ι ΐΨί”κ÷°«ΑΒΡ ΐΨίΚœ≤ΔΚσΘ§ΖΔœ÷≤α ΐΒΡ÷–ΈΜ ΐΟΜΗΡ±δΘ§«σΉνΕύ≤Ι≤ιΝΥΦΗ»ΥΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©9Θ§5≤αΘΜΘ®2Θ©135ΓψΘΜΘ®3Θ©![]() ΘΜΘ®4Θ©Ήή»Υ ΐ≤ΜΡή≥§Ιΐ27Θ§Φ¥ΉνΕύ≤Ι≤ιΝΥ3»ΥΘ°
ΘΜΘ®4Θ©Ήή»Υ ΐ≤ΜΡή≥§Ιΐ27Θ§Φ¥ΉνΕύ≤Ι≤ιΝΥ3»ΥΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©”…6≤α»Υ ΐΦΑΤδΥυ’ΦΑΌΖ÷±»«σ≥ωΉή»Υ ΐΘ§‘ΌΗυΨίΗς≤α ΐΒΡ»Υ ΐΚΆΒ»”ΎΉή»Υ ΐΩ…ΒΟ5≤α»Υ ΐΘΜ
Θ®2Θ©”Ο360Γψ≥Υ“‘Ε‘”Π»Υ ΐΥυ’Φ±»άΐΦ¥Ω…ΒΟΘΜ
Θ®3Θ©ΗυΨίΗ≈¬ ΙΪ Ϋ”Ο6≤αΓΔ7≤α»Υ ΐΚΆ≥ΐ“‘Ήή»Υ ΐΦ¥Ω…ΒΟΘΜ
Θ®4Θ©”…4≤αΚΆ5≤αΒΡ»Υ ΐΚΆΈΣ14Θ§÷–ΈΜ ΐΟΜ”–ΗΡ±δ÷ΣΉή»Υ ΐ≤ΜΡή≥§Ιΐ27Θ§Ψί¥ΥΩ…ΒΟ¥πΑΗΘ°
ΫβΘΚΘ®1Θ©ΓΏ±ΜΒς≤ιΒΡΉή»Υ ΐΈΣ6Γ¬25%ΘΫ24Θ®»ΥΘ©Θ§
Γύ5≤αΒΡ»Υ ΐΈΣ24©¹Θ®5+6+4Θ©ΘΫ9Θ®»ΥΘ©Θ§
±Μ≥ι•ΥΒΡ―ß…ζΕΝ ι≤α ΐΒΡ÷–ΈΜ ΐ «ΒΎ12ΓΔ13Ηω ΐΨίΒΡΤΫΨυ ΐΘ§ΕχΒΎ12ΓΔ13Ηω ΐΨίΨυΈΣ5≤αΘ§
Γύ±Μ≥ι•ΥΒΡ―ß…ζΕΝ ι≤α ΐΒΡ÷–ΈΜ ΐΈΣ5≤αΘ§
Ι ¥πΑΗΈΣ9»ΥΘ§5≤αΘΜ
Θ®2Θ©…»–ΈΆΦ÷–5≤αΥυ’ΦΒΡ‘≤–ΡΫ«ΒΡΕ» ΐΈΣ360ΓψΓΝ![]() ΘΫ135ΓψΘ§
ΘΫ135ΓψΘ§
Ι ¥πΑΗΈΣ135ΓψΘΜ
Θ®3Θ©―Γ÷–ΕΝ ι≥§Ιΐ5≤αΒΡ―ß…ζΒΡΗ≈¬ ΈΣ![]() ΘΜ
ΘΜ
Θ®4Θ©ΓΏ4≤αΚΆ5≤αΒΡ»Υ ΐΚΆΈΣ14Θ§÷–ΈΜ ΐΟΜ”–ΗΡ±δΘ§
ΓύΉή»Υ ΐ≤ΜΡή≥§Ιΐ27Θ§Φ¥ΉνΕύ≤Ι≤ιΝΥ3»ΥΘ°

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ