题目内容
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 点位于
点位于![]() 点左侧),与
点左侧),与![]() 轴交于
轴交于![]() 点,连接
点,连接![]() .点
.点![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 为
为![]() .
.

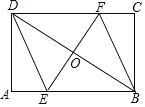
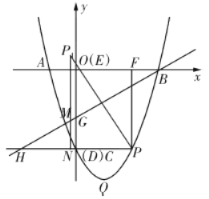
(1)点![]() 是第四象限内抛物线上的一点,过点
是第四象限内抛物线上的一点,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,作
,作![]() 轴于点
轴于点![]() ,作
,作![]() 轴于点
轴于点![]() ,点
,点![]() 在点
在点![]() 右边.点
右边.点![]() 是直线
是直线![]() 上一个动点,点
上一个动点,点![]() 是直线
是直线![]() 上一个动点,当四边形
上一个动点,当四边形![]() 的周长最大时,求
的周长最大时,求![]() 的最小值;
的最小值;
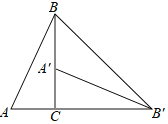
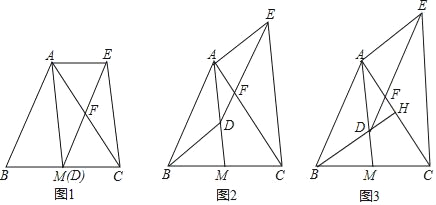
(2)如图2,将原抛物线绕其对称轴与![]() 轴的交点
轴的交点![]() 旋转
旋转![]() 得新的抛物线
得新的抛物线![]() ,点
,点![]() ,
,![]() 的对应点分别记为
的对应点分别记为![]() ,
,![]() ,把抛物线
,把抛物线![]() 沿直线
沿直线![]() 平移,
平移,![]() ,
,![]() 的对应点分别记为
的对应点分别记为![]() ,
,![]() 是否存在点
是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为腰的等腰三角形?若存在,请直接写出
为腰的等腰三角形?若存在,请直接写出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() 的最小值为
的最小值为![]() ;(2)存在,
;(2)存在,![]() 或
或![]() 或
或![]() .
.
【解析】
(1) 设 ,则
,则![]() .然后再确定抛物线的对称轴以及开口方向,即可确定最值;
.然后再确定抛物线的对称轴以及开口方向,即可确定最值;
(2)由题意知,抛物线绕其对称轴与![]() 轴的交点
轴的交点![]() 旋转
旋转![]() 得抛物线
得抛物线![]() ,点
,点![]() 的对应
的对应![]() 与点
与点![]() 重合.设
重合.设![]() ,
,![]() ,然后利用勾股定理得到
,然后利用勾股定理得到![]() ;然后就
;然后就![]() 和
和![]() 分别解答即可.
分别解答即可.
解:(1)![]() ,
,![]() ,
,![]() ,
,![]() .
.
设 ,则
,则![]() .
.
![]() 抛物线
抛物线![]() 的对称轴为
的对称轴为![]() ,
,
![]() .
.
![]() 矩形
矩形![]() 的周长
的周长![]()
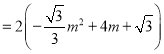
![]() .
.
此函数的图象为抛物线,其对称轴为![]() ,且
,且![]() .
.
![]() ,
,
![]() 当
当![]() 时,矩形
时,矩形![]() 的周长最大,此时点
的周长最大,此时点![]() 的坐标为
的坐标为![]() .
.
作点![]() 关于
关于![]() 的对称点
的对称点![]() ,
,
![]() ,
,
![]() 作
作![]() 于
于![]() 交
交![]() 于
于![]() ,此时
,此时![]() 最小,
最小,![]() 的最小值
的最小值![]() .
.
延长![]() 交
交![]() 于
于![]() ,可求得
,可求得![]() ,
,![]() ,
,
![]() 的最小值
的最小值![]() .
.
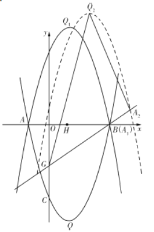
(2)由题意知,抛物线绕其对称轴与![]() 轴的交点
轴的交点![]() 旋转
旋转![]() 得抛物线
得抛物线![]() ,点
,点![]() 的对应
的对应![]() 与点
与点![]() 重合.
重合.
设![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,
①当![]() 时,
时,![]()
即![]()
![]() .
.
化简后解得![]() .
.
②当![]() 时,
时,![]() ,
,
即![]() .
.
化简后解得![]() .
.
综上所述,![]() 或
或![]() 或
或![]() .
.

【题目】某年级共有![]() 名学生.为了解该年级学生
名学生.为了解该年级学生![]() ,
,![]() 两门课程的学习情况,从中随机抽取
两门课程的学习情况,从中随机抽取![]() 名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理描述和分析下面给出了部分信息.
名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理描述和分析下面给出了部分信息.
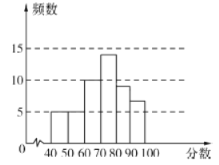
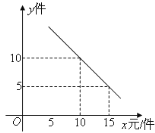
①![]() 课程成绩的频数分布直方图如下(数据分成
课程成绩的频数分布直方图如下(数据分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() );
);
②![]() 课程成绩在
课程成绩在![]() 这一组的数据为:
这一组的数据为:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
③![]() ,
,![]() 两门课程成绩的平均数、中位数、众数如下:
两门课程成绩的平均数、中位数、众数如下:
课程 | 平均数 | 中位数 | 众数 |
|
|
|
|
|
|
|
|
根据以上信息,回答下列问题:
(1)写出表中![]() 的值;
的值;
(2)在此次测试中,某学生的![]() 课程成绩为
课程成绩为![]() 分,
分,![]() 课程成绩为
课程成绩为![]() 分,这名学生成绩排名更靠前的课程是_______(填“
分,这名学生成绩排名更靠前的课程是_______(填“![]() ”或“
”或“![]() ”),理由是;___________;
”),理由是;___________;
(3)假设该年级学生都参加了此次测试,估计![]() 课程成绩超过
课程成绩超过![]() 分的人数.
分的人数.
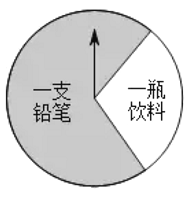
【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物![]() 元以上可以获得一次转动转 盘的机会,当转盘停止时指针落在哪一个区域就获得相应的奖品 (指针指向两个扇形的交线时,当作指向右边的扇形),下表是活动进行中的一组统计数据:
元以上可以获得一次转动转 盘的机会,当转盘停止时指针落在哪一个区域就获得相应的奖品 (指针指向两个扇形的交线时,当作指向右边的扇形),下表是活动进行中的一组统计数据:
转动转盘的次数 |
|
|
|
|
|
|
落在“铅笔"的次数 |
|
|
|
|
|
|
落在“铅笔"的频率 |
|
|
|
|
|
|
(1)转动该转盘一次,获得铅笔的概率约为____ ;( 结果保留小数点后一位数字);
(2)铅笔每只![]() 元,饮料每瓶
元,饮料每瓶![]() 元,经统计该商场每天约有
元,经统计该商场每天约有![]() 名顾各参加抽奖活动,请计算该商场每天需要支出的奖品费用;
名顾各参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在![]() 元左右,则转盘上“一瓶饮料”区域的圆心角应调整为 度.
元左右,则转盘上“一瓶饮料”区域的圆心角应调整为 度.