题目内容
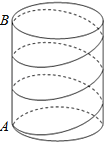
【题目】如图，圆柱底面半径为
cm，高为18cm，点A、B分别是圆柱两底面圆周上的点，且A、B在同一母线上，用一根棉线从A点顺着圆柱侧面绕3圈到B点，则这根棉线的长度最短为（ ）
A.24cmB.30cmC.2
cmD.4
cm
【答案】B
【解析】
要求圆柱体中两点之间的最短路径，最直接的作法，就是将圆柱体展开，然后利用两点之间线段最短解答．
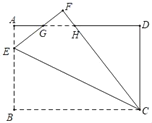
解：圆柱体的展开图如图所示：用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是：AC→CD→DB；
即在圆柱体的展开图长方形中，将长方形平均分成3个小长方形，A沿着3个长方形的对角线运动到B的路线最短；
∵圆柱底面半径为
cm，
∴长方形的宽即是圆柱体的底面周长：2π×＝8cm；
又∵圆柱高为18cm，
∴小长方形的一条边长是6cm；
根据勾股定理求得AC＝CD＝DB＝10cm；
∴AC+CD+DB＝30cm；
故选：B．
练习册系列答案
阶梯计算系列答案
相关题目
【题目】4月23日为“世界读书日”，每年的这一天，世界100多个国家都会举办各种各样的庆祝和图书宣传活动．我县某书店借此机会决定开展“读书节”活动，为迎接“读书节”制定了活动计划．以下是活动计划书的部分信息：
“读书节”活动计划书 | ||
图书类別 | A类 | B类 |
进价（元/本） | 18 | 12 |
备注 | （1）用不超过16800元购进A、B两类图书共1000本： （2）A类图书不少于600本： | |
（1）陈经理査看计划书时发现：A类图书的标价是B类图书标价的1.5倍，若顾客同样用540元购买图书，能购买A类图书数量比B类图书的数量少10本，请求出A、B两类图书的标价；
（2）经市场调查后，陈经理发现它们高估了“读书节”对图书销售的影响：便调整了销售方案；A类图书每本按标价降低2元销售，B类图书价格不变，那么该书店应如何进货才能获得最大利润？
