题目内容
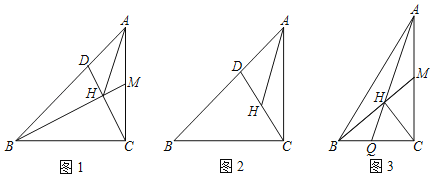
【题目】如图,在Rt△ABC中,![]() =n,M为BC上的一点,连接BM.
=n,M为BC上的一点,连接BM.
(1)如图1,若n=1,
①当M为AC的中点,当BM⊥CD于H,连接AH,求∠AHD的度数;
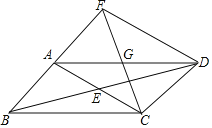
②如图2,当H为CD的中点,∠AHD=45°,求![]() 的值和∠CAH的度数;
的值和∠CAH的度数;
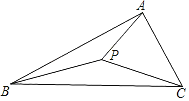
(2)如图3,CH⊥AM于H,连接CH并延长交AC于Q,M为AC中点,直接写出tan∠BHQ的值(用含n的式子表示).
【答案】(1)①45°;②![]() ,15°;(2)tan∠BHQ=n.
,15°;(2)tan∠BHQ=n.
【解析】
(1)①如图1中,作AK⊥CD交CD的延长线于K.利用全等三角形的性质证明AK=CH,再证明CH=KH,推出AK=KH即可解决问题.
②如图2中,作AK⊥CD交CD的延长线于K,作CM⊥AB于M.设DH=CH=a.证明△ADH∽△CDA,推出AD=![]() a,设AM=CM=BM=x,在Rt△CMD中,根据CM2=DM2+CD2,构建方程求出x(用a表示),求出BD即可,再证明sin∠ACK=
a,设AM=CM=BM=x,在Rt△CMD中,根据CM2=DM2+CD2,构建方程求出x(用a表示),求出BD即可,再证明sin∠ACK=![]() ,推出∠ACK=30°即可解决问题.
,推出∠ACK=30°即可解决问题.
(2)作AJ⊥BM交BM的延长线于J.设AM=CM=y,则BC=2yn.想办法求出AJ,HJ(用n,y表示)即可解决问题.
(1)①如图1中,作AK⊥CD交CD的延长线于K.

∵CD⊥BM,AK⊥CK,∠ACB=90°,
∴∠CHB=∠K=90°,∠CBH+∠BCH=90°,∠BCH+∠ACK=90°,
∴∠CBH=∠ACK,
∵CB=CA,
∴△CHB≌△AKC(AAS),
∴AK=CH,
∵∠CHM=∠K=90°,
∴MH∥AK,
∵AM=BM,
∴CH=KH,
∴AK=KH,
∵∠K=90°,
∴∠AHD=45°.
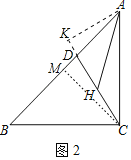
②如图2中,作AK⊥CD交CD的延长线于K,作CM⊥AB于M.设DH=CH=a.
∵CA=CB,∠ACB=90°,
∴∠CAB=45°,
∵∠AHD=45°,∠AHD=∠ACH+∠CAH,
∴∠ACH+∠CAH=∠CAH+∠DAH,
∴∠DAH=∠ACD,
∵∠ADH=∠CAD,
∴△ADH∽△CDA,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AD=![]() a,
a,
∵CA=CB,∠ACB=90°,CM⊥AB,
∴AM=BM,
∴CM=AM=BM,设AM=CM=BM=x,
在Rt△CMD中,∵CM2=DM2+CD2,
∴x2+(x﹣![]() a)2=4a2,
a)2=4a2,
解得x=![]() a(负根已经舍弃).
a(负根已经舍弃).
∴BD=AB﹣AD=(![]() +
+![]() )a﹣
)a﹣![]() a=
a=![]() a,
a,
∴![]() .
.
∵△ADH∽△CDA,
∴![]() ,设AH=m,则AC=
,设AH=m,则AC=![]() m,AK=KH=
m,AK=KH=![]() m,
m,
∴tan∠ACK=![]() ,
,
∴∠ACH=30°,
∴∠CAH=∠AHD﹣∠ACH=45°﹣30°=15°.
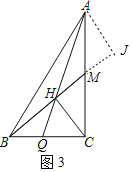
(2)作AJ⊥BM交BM的延长线于J.设AM=CM=y,则BC=2yn.
∵CH⊥BM,BM=![]() =
=![]() =
=![]() y,
y,
∴CH=![]() =
=![]() ,
,
∴HM=![]() =
=![]() y,
y,
∵AJ⊥BJ,CH⊥BJ,
∴∠J=∠CHM=90°,
∵∠AMJ=∠CMH,AM=CM,
∴△AMJ≌△CMH(AAS),
∴AJ=CH=![]() y,HM=JM=
y,HM=JM=![]() y,
y,
∵∠BHQ=∠AHJ,
∴tan∠BHQ=tan∠AHJ=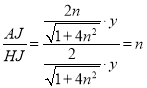 .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】某年级共有![]() 名学生.为了解该年级学生
名学生.为了解该年级学生![]() ,
,![]() 两门课程的学习情况,从中随机抽取
两门课程的学习情况,从中随机抽取![]() 名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理描述和分析下面给出了部分信息.
名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理描述和分析下面给出了部分信息.
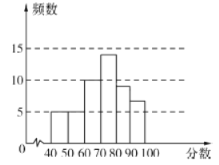
①![]() 课程成绩的频数分布直方图如下(数据分成
课程成绩的频数分布直方图如下(数据分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() );
);
②![]() 课程成绩在
课程成绩在![]() 这一组的数据为:
这一组的数据为:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
③![]() ,
,![]() 两门课程成绩的平均数、中位数、众数如下:
两门课程成绩的平均数、中位数、众数如下:
课程 | 平均数 | 中位数 | 众数 |
|
|
|
|
|
|
|
|
根据以上信息,回答下列问题:
(1)写出表中![]() 的值;
的值;
(2)在此次测试中,某学生的![]() 课程成绩为
课程成绩为![]() 分,
分,![]() 课程成绩为
课程成绩为![]() 分,这名学生成绩排名更靠前的课程是_______(填“
分,这名学生成绩排名更靠前的课程是_______(填“![]() ”或“
”或“![]() ”),理由是;___________;
”),理由是;___________;
(3)假设该年级学生都参加了此次测试,估计![]() 课程成绩超过
课程成绩超过![]() 分的人数.
分的人数.
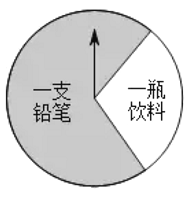
【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物![]() 元以上可以获得一次转动转 盘的机会,当转盘停止时指针落在哪一个区域就获得相应的奖品 (指针指向两个扇形的交线时,当作指向右边的扇形),下表是活动进行中的一组统计数据:
元以上可以获得一次转动转 盘的机会,当转盘停止时指针落在哪一个区域就获得相应的奖品 (指针指向两个扇形的交线时,当作指向右边的扇形),下表是活动进行中的一组统计数据:
转动转盘的次数 |
|
|
|
|
|
|
落在“铅笔"的次数 |
|
|
|
|
|
|
落在“铅笔"的频率 |
|
|
|
|
|
|
(1)转动该转盘一次,获得铅笔的概率约为____ ;( 结果保留小数点后一位数字);
(2)铅笔每只![]() 元,饮料每瓶
元,饮料每瓶![]() 元,经统计该商场每天约有
元,经统计该商场每天约有![]() 名顾各参加抽奖活动,请计算该商场每天需要支出的奖品费用;
名顾各参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在![]() 元左右,则转盘上“一瓶饮料”区域的圆心角应调整为 度.
元左右,则转盘上“一瓶饮料”区域的圆心角应调整为 度.