题目内容
【题目】如图,在Rt△ABC中,∠C = 90°,点O是斜边AB上一定点,到点O的距离等于OB的所有点组成图形W,图形W与AB,BC分别交于点D,E,连接AE,DE,∠AED=∠B.

(1)判断图形W与AE所在直线的公共点个数,并证明.
(2)若![]() ,
,![]() ,求OB.
,求OB.
【答案】(1)有一个公共点,证明见解析;(2)![]() .
.
【解析】
(1)先根据题意作出图形W,再作辅助线,连接OE,证明AE是圆O的切线即可;
(2)先利用解直角三角形的知识求出CE=1,从而求出BE=3.再由AC∥DE 得出![]() ,把各线段的长代入即可求出OB的值.
,把各线段的长代入即可求出OB的值.
(1)判断有一个公共点
证明:连接OE,如图.
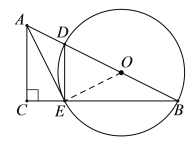
∵ BD是⊙O的直径,
∴ ∠DEB=90°.
∵ OE=OB,
∴ ∠OEB=∠B.
又∵∠AED=∠B,
∴ ∠AED=∠OEB.
∴ ∠AEO =∠AED+∠DEO
=∠OEB +∠DEO
=∠DEB=90°.
∴ AE是⊙O的切线.
∴图形W与AE所在直线有1个公共点.
(2)解:∵ ∠C = 90°,![]() ,
,![]() ,
,
∴ AC=2,![]() .
.
∵ ∠DEB=90°,
∴ AC∥DE.
∴ ![]() ∠CA E=
∠CA E=![]() ∠AED=
∠AED=![]() B
B ![]() .
.
在Rt△ACE中,∠C = 90°,AC=2,
∴ CE=1.
∴ BE=3.
∵AC∥DE
∴![]() .
.
∴![]() ,
,
∴![]() .
.

【题目】下表是某班同学随机投掷一枚硬币的试验结果.
抛掷次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
“正面向上”次数 | 22 | 52 | 68 | 101 | 116 | 147 | 160 | 187 | 214 | 238 |
“正面向上”频率 | 0.44 | 0.52 | 0.45 | 0.51 | 0.46 | 0.49 | 0.46 | 0.47 | 0.48 | 0.48 |
下面有三个推断:
①表中没有出现“正面向上”的频率是0.5的情况,所以不能估计“正面向上”的概率是0.5;
②这些次试验投掷次数的最大值是500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生;
其中合理的是__________(填写序号).