题目内容
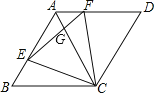
【题目】如图,已知四边形ABDE是平行四边形,C为边B D延长线上一点,连结AC、CE,使AB=AC.
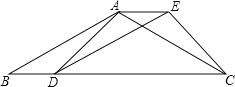
(1)求证:△BAD≌△AEC;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)应用平行四边形的性质由SAS证明△DBA≌△AEC.
(2)过A作AG⊥BC,垂足为G,设AG=x,首先根据锐角三角函数关系得出![]() ,进而利用BG-DG=BD求出AG的长,进而得出平行四边形ABDE的面积.
,进而利用BG-DG=BD求出AG的长,进而得出平行四边形ABDE的面积.
解:(1)∵AB=AC, ∴∠B=∠ACB.
又∵四边形ABDE是平行四边形,∴AE∥BD,AE=BD.
∴∠ACB=∠CAE=∠B.
在△DBA和△AEC中,∵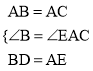 ,
,
∴△DBA≌△AEC(SAS).
(2)过A作AG⊥BC,垂足为G.设AG=x,
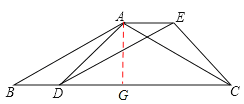
在Rt△AGD中,∵∠ADC=45°,∴AG=DG=x.
在Rt△AGB中,∵∠B=30°,∴![]() .
.
又∵BD=10,
∴BG-DG=BD,即![]() ,解得
,解得![]() .
.
∴![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
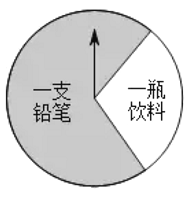
【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物![]() 元以上可以获得一次转动转 盘的机会,当转盘停止时指针落在哪一个区域就获得相应的奖品 (指针指向两个扇形的交线时,当作指向右边的扇形),下表是活动进行中的一组统计数据:
元以上可以获得一次转动转 盘的机会,当转盘停止时指针落在哪一个区域就获得相应的奖品 (指针指向两个扇形的交线时,当作指向右边的扇形),下表是活动进行中的一组统计数据:
转动转盘的次数 |
|
|
|
|
|
|
落在“铅笔"的次数 |
|
|
|
|
|
|
落在“铅笔"的频率 |
|
|
|
|
|
|
(1)转动该转盘一次,获得铅笔的概率约为____ ;( 结果保留小数点后一位数字);
(2)铅笔每只![]() 元,饮料每瓶
元,饮料每瓶![]() 元,经统计该商场每天约有
元,经统计该商场每天约有![]() 名顾各参加抽奖活动,请计算该商场每天需要支出的奖品费用;
名顾各参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在![]() 元左右,则转盘上“一瓶饮料”区域的圆心角应调整为 度.
元左右,则转盘上“一瓶饮料”区域的圆心角应调整为 度.