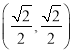ЬтФПФкШн
ЁОЬтФПЁПвбжЊХзЮяЯпгы![]() жсНЛгк
жсНЛгк![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() .
.
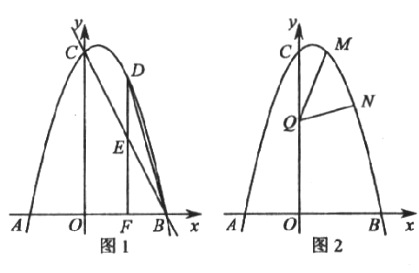
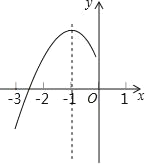
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФБэДяЪНМАЖЅЕуЕФзјБъЃЛ
ЃЈ2ЃЉШєЕу![]() ЪЧ
ЪЧ![]() жсЩЯЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЈгыЕу
жсЩЯЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЈгыЕу![]() ВЛжиКЯЃЉЃЌЙ§Еу
ВЛжиКЯЃЉЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() .ЩшЕу
.ЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() .
.
ЂйЪдгУКЌ![]() ЕФДњЪ§ЪНБэЪО
ЕФДњЪ§ЪНБэЪО![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЂкжБЯп![]() ФмЗёАб
ФмЗёАб![]() ЗжГЩУцЛ§жЎБШЮЊ1ЃК2ЕФСНВПЗжЃПШєФмЃЌЧыЧѓГіЕу
ЗжГЩУцЛ§жЎБШЮЊ1ЃК2ЕФСНВПЗжЃПШєФмЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩ.
ЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩ.
ЃЈ3ЃЉШчЭМ2ЃЌШєЕу![]() вВдкДЫХзЮяЯпЩЯЃЌЮЪдк
вВдкДЫХзЮяЯпЩЯЃЌЮЪдк![]() жсЩЯЪЧЗёДцдкЕу
жсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃПШєДцдкЃЌЧыжБНгаДГіЕу
ЃПШєДцдкЃЌЧыжБНгаДГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
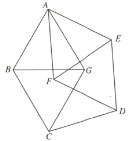
ЁОД№АИЁПЃЈ1ЃЉ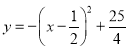 ЃЌЖЅЕузјБъЮЊЃК
ЃЌЖЅЕузјБъЮЊЃК![]() ЃЛЃЈ2ЃЉЂй
ЃЛЃЈ2ЃЉЂй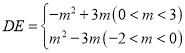 ЃЛЂкФмЃЌРэгЩМћНтЮіЃЌЕу
ЃЛЂкФмЃЌРэгЩМћНтЮіЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЛЃЈ3ЃЉДцдкЃЌЕуQЕФзјБъЮЊЃК
ЃЛЃЈ3ЃЉДцдкЃЌЕуQЕФзјБъЮЊЃК![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіХзЮяЯпЕФНтЮіЪНЃЌШЛКѓАбвЛАуЪНзЊЛЏЮЊЖЅЕуЪНМДПЩЕУГіХзЮяЯпЕФЖЅЕузјБъЃЛ
ЃЈ2ЃЉЂйЯШРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯп![]() ЕФКЏЪ§БэДяЪНЃЌдйЩшГіЕуDЁЂEЕФзјБъЃЌШЛКѓЗжЕуDдкyжсгвВрКЭyжсзѓВрРћгУ
ЕФКЏЪ§БэДяЪНЃЌдйЩшГіЕуDЁЂEЕФзјБъЃЌШЛКѓЗжЕуDдкyжсгвВрКЭyжсзѓВрРћгУ![]() Лђ
Лђ![]() СаЪНЛЏМђМДПЩЃЛ
СаЪНЛЏМђМДПЩЃЛ
ЂкИљОнЬтвтШнвзХаЖЯЃКЕуDдкyжсзѓВрЪБЃЌВЛДцдкетбљЕФЕу![]() ЃЛЕБЕуDдкyжсгвВрЪБЃЌЗж
ЃЛЕБЕуDдкyжсгвВрЪБЃЌЗж![]() Лђ
Лђ![]() СНжжЧщПіЃЌЩшГіEЁЂFзјБъКѓЃЌСаГіЗНГЬЧѓНтМДПЩЃЛ
СНжжЧщПіЃЌЩшГіEЁЂFзјБъКѓЃЌСаГіЗНГЬЧѓНтМДПЩЃЛ
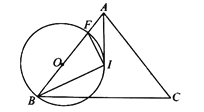
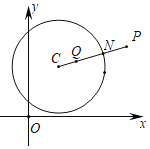
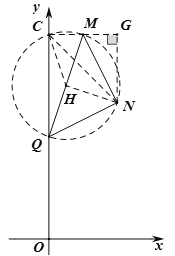
ЃЈ3ЃЉЯШЧѓЕУЕуMЁЂNЕФзјБъЃЌШЛКѓСЌНгCMЃЌЙ§ЕуNзїNGЁЭCMНЛCMЕФбгГЄЯпгкЕуGЃЌМДПЩХаЖЯЁЯMCN=45ЁуЃЌдђЕуCМДЮЊЗћКЯЬтвтЕФвЛИіЕуQЃЌЫљвдСэвЛжжЧщПіЕФЕуQгІЮЊЙ§ЕуCЁЂMЁЂNЕФЁбHгыyжсЕФНЛЕуЃЌШЛКѓИљОндВжмНЧЖЈРэЕФЭЦТлЁЂЕШбќжБНЧШ§НЧаЮЕФаджЪКЭЙДЙЩЖЈРэМДПЩЧѓГіCQЕФГЄЃЌНјЖјПЩЕУНсЙћ.
НтЃКЃЈ1ЃЉЁпХзЮяЯпгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌ
ЃЌ
ЁрЩшХзЮяЯпЕФБэДяЪНЮЊЃК![]() ЃЌ
ЃЌ
АбЕу![]() ДњШыВЂЧѓЕУЃК
ДњШыВЂЧѓЕУЃК![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФБэДяЪНЮЊЃК![]()
![]() ЃЌ
ЃЌ
МД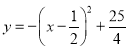 ЃЌЁрХзЮяЯпЕФЖЅЕузјБъЮЊЃК
ЃЌЁрХзЮяЯпЕФЖЅЕузјБъЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйЩшжБЯп![]() ЕФБэДяЪНЮЊЃК
ЕФБэДяЪНЮЊЃК![]() ЃЌдђ
ЃЌдђ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯп![]() ЕФБэДяЪНЮЊЃК
ЕФБэДяЪНЮЊЃК![]() ЃЌ
ЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌЁр
ЪБЃЌЁр![]()
![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
![]() ЃЌ
ЃЌ
злЩЯЃК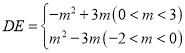 ЃЌ
ЃЌ
ЂкгЩЬтвтжЊЃКЕБ![]() ЪБЃЌВЛДцдкетбљЕФЕу
ЪБЃЌВЛДцдкетбљЕФЕу![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЈЩсШЅЃЉЃЌЁр
ЃЈЩсШЅЃЉЃЌЁр![]() ЃЌ
ЃЌ
Лђ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
злЩЯЃЌжБЯп![]() ФмАб
ФмАб![]() ЗжГЩУцЛ§жЎБШЮЊ1ЃК2ЕФСНВПЗжЃЌЧвЕу
ЗжГЩУцЛ§жЎБШЮЊ1ЃК2ЕФСНВПЗжЃЌЧвЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁпЕу![]() дкХзЮяЯп
дкХзЮяЯп![]() ЩЯЃЌЁр
ЩЯЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
СЌНгMCЃЌШчЭМЃЌЁпCЃЈ0ЃЌ6ЃЉЃЌMЃЈ1ЃЌ6ЃЉЁрMCЁЭyжсЃЌЙ§ЕуNзїNGЁЭCMНЛCMЕФбгГЄЯпгкЕуGЃЌЁпNЃЈ2ЃЌ4ЃЉЃЌЁрCG=NG=2ЃЌЁрЁїCNGЪЧЕШбќжБНЧШ§НЧаЮЃЌЁрЁЯMCN=45ЁуЃЌдђЕуCМДЮЊЗћКЯЬтвтЕФвЛИіЕуQЃЌЁрСэвЛжжЧщПіЕФЕуQгІЮЊЙ§ЕуCЁЂMЁЂNЕФЁбHгыyжсЕФНЛЕуЃЌСЌНгHNЃЌ
Ёп![]() ЃЌЁрMN=
ЃЌЁрMN=![]() ЃЌCM=1ЃЌ
ЃЌCM=1ЃЌ
Ёп![]() ЃЌЁрЁЯMHN=90ЁуЃЌдђАыОЖMH=NH=
ЃЌЁрЁЯMHN=90ЁуЃЌдђАыОЖMH=NH=![]() ЃЌ
ЃЌ
ЁпЁЯMCQ=90ЁуЃЌЁрMQЪЧжБОЖЃЌЧв![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
ЁпOC=6ЃЌЁрOQ=3ЃЌЁрQЃЈ0ЃЌ3ЃЉЃЛ
злЩЯЃЌдк![]() жсЩЯДцдкЕу
жсЩЯДцдкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЧвЕуQЕФзјБъЮЊЃК
ЃЌЧвЕуQЕФзјБъЮЊЃК![]() Лђ
Лђ![]() .
.

 ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ
ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИ
вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИ