题目内容
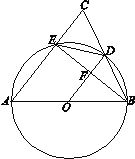
【题目】如图,在![]() 中,
中,![]() 是内心,
是内心,![]() ,
,![]() 是
是![]() 边上一点,以点
边上一点,以点![]() 为圆心,
为圆心,![]() 为半径的
为半径的![]() 经过点
经过点![]() ,交
,交![]() 于点
于点![]() .
.
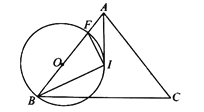
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)连接![]() ,若
,若![]() ,
,![]() ,求圆心
,求圆心![]() 到
到![]() 的距离及
的距离及![]() 的长.
的长.
【答案】(1)见解析;(2)点![]() 到
到![]() 的距离是1,
的距离是1,![]() 的长度
的长度![]()
【解析】
(1)连接OI,延长AI交BC于点D,根据内心的概念及圆的性质可证明OI∥BD,再根据等腰三角形的性质及平行线的性质可证明∠AIO=90°,从而得到结论;
(2)过点O作OE⊥BI,利用垂径定理可得到OE平分BI,再根据圆的性质及中位线的性质即可求出O到BI的距离;根据角平分线及圆周角定理可求出∠FOI=60°,从而证明△FOI为等边三角形,最后利用弧长公式进行计算即可.
解:(1)证明:延长AI交BC于D,连接OI,
∵I是△ABC的内心,
∴BI平分∠ABC,AI平分∠BAC,
∴∠1=∠3,
又∵OB=OI,
∴∠3=∠2,
∴∠1=∠2,
∴OI∥BD,
又∵AB=AC,
∴AD⊥BC,即∠ADB=90°,
∴∠AIO=∠ADB=90°,
∴AI为![]() 的切线;
的切线;
(2)作OE⊥BI,由垂径定理可知,OE平分BI,
又∵OB=OF,
∴OE是△FBI的中位线,
∵IF=2,
∴OE=![]() IF=
IF=![]() =1,
=1,
∴点O到BI的距离是1,
∵∠IBC=30°,
由(1)知∠ABI=∠IBC,
∴∠ABI =30°,
∴∠FOI=60°,
又∵OF=OI,
∴△FOI是等边三角形,
∴OF=OI=FI=2,
∴![]() 的长度
的长度![]() .
.


练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目