��Ŀ����
����Ŀ��ijУΪ����������չ����л�ͬѧ����ʦ��������һЩˮ�ʺ����Ϻ���Ϊ��Ʒ���������ͼ����������Ϣ������������⣻ 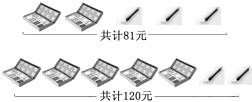
��1�����ÿ�����ϺУ�ÿ֧ˮ�ʸ�����Ԫ��
��2����ѧУ�ƻ��������Ϻк�ˮ�ʹ�20�������÷��ò�����340Ԫ�������Ϻ��������ٸ���
��3��ǡ���̵�����Żݴ����������취���£����Ϻа������Żݣ�ˮ��10֧���ϳ������ְ������Żݣ���ѧУ��������ͬ��������ͬһ��Ʒ�����Ҹý�Ʒ����������10������������������������Ϻк��㻹�ǹ���ˮ�ʺ��㣮
���𰸡�
��1���⣺��ÿ�����Ϻ�ΪxԪ��ÿ֧ˮ��ΪyԪ��
��������ã� ![]() ��
��
��� ![]() ��
��
��ÿ�����Ϻ�Ϊ18Ԫ��ÿ֧ˮ��Ϊ15Ԫ��
��2���⣺�蹺�����Ϻ�a������ˮ��Ϊ20��a����������ã�
18a+15��20��a����340��
���a��13 ![]() ��
��
�������Ϻ������13����
��3���⣺�蹺�������Ϊm������m��10��
������֪���������Ϻ�y1����m�ĺ�����ϵʽ��y1=18��70%m��
��y1=12.6m��
����ˮ��y2=15��10+15����m��10����80%��
��y2=30+12m��
��y1=y2ʱ����12m+30=12.6mʱ�����m=50��
��y1��y2ʱ����12.6m��12m+30ʱ�����m��50��
��y1��y2ʱ����12.6m��12m+30ʱ�����m��50��
����������������Ʒ����10��������50��ʱ�������Ϻк��㣮
������Ʒ����50��ʱ����ˮ�ʺ����Ϻ�Ǯ����ͬ��
����������1����ÿ�����Ϻ�ΪxԪ��ÿ֧ˮ��ΪyԪ��Ȼ���г���������⼴�ɣ���2���蹺�����Ϻ�a������ˮ��Ϊ20��a�����������÷��ò�����340Ԫ�г�����ʽ������⣻��3���蹺�������Ϊm�����г���������ʽ�������������ʽ�������Ʒ������Ȼ��д���������ɣ�

����Ŀ��Ϊ�ƽ���ȫ������ѧ�����������˶�����ʵʩ����֯���ͬѧ��չ�������ϵĵڶ����û������ij��ѧ���齨�������ţ�����������ë��ƹ�����赸���š����������š��������ţ�Ϊ�˽���Уѧ������4�����Ż��ϲ���������У�����ȡ���ֳ����������ˡ�����ϲ���ĸ����š����飬����������ݻ��Ƴ����²�������ͳ�Ʊ��������ͼ���е���Ϣ����������⣺
������� | ���� | ռ���������� |
���� | 60 | m |
�赸 | 30 | 0.25 |
������ | n | 0.15 |
���� | 12 | 0.1 |

��1��������������������m��n��ֵ��
��2���벹ȫͳ��ͼ��
��3���������60��ϲ������ͬѧ����3����ϲ����������У��3000��ѧ��������Ƹ�У��ϲ�������������