题目内容
【题目】细观察，找规律
下列各图中的MA1与NAn平行．
（1）图①中的∠A1+∠A2= ______ 度，
图②中的∠A1+∠A2+∠A3= ______ 度，
图③中的∠A1+∠A2+∠A3+∠A4= ______ 度，
图④中的∠A1+∠A2+∠A3+∠A4+∠A5= ______ 度，
…，
第⑩个图中的∠A1+∠A2+∠A3+…+∠A11= ______ 度
（2）第n个图中的∠A1+∠A2+∠A3+…+∠An+1= ______
（3）请你证明图②的结论．
【答案】180， 360， 540， 720， 1800； （2）180n度；（3）见解析.
【解析】
（1）首先过各点作MA1的平行线，由MA1∥NA2，可得各线平行，根据两直线平行，同旁内角互补，即可得到结论；
（2）根据（1）中的规律，即可得到第n个图中的∠A1+∠A2+∠A3+…+∠An+1的度数；
（3）先过A2作A2B∥A1M，根据A2B∥A1M∥A3N，可得∠A1+∠1=180°，∠A3+∠2=180°，进而得出∠A1+∠A1A2A3+∠A3=360°．
解：（1）
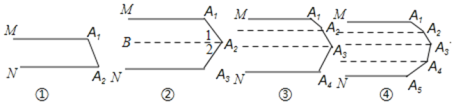
根据平行线的性质，可得图①中的∠A1+∠A2=180度，
根据平行线的性质，可得图②中的∠A1+∠A2+∠A3=360度，
根据平行线的性质，可得图③中的∠A1+∠A2+∠A3+∠A4=540度，
根据平行线的性质，可得图④中的∠A1+∠A2+∠A3+∠A4+∠A5=720度；
…，
根据平行线的性质，可得第⑩个图中的∠A1+∠A2+∠A3+…+∠A11= 1800 度
（2）根据平行线的性质，可得第n个图中的∠A1+∠A2+∠A3+…+∠An+1=180n度；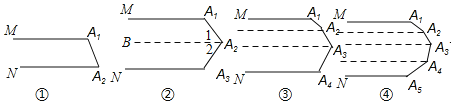
（3）如图②，过A2作A2B∥A1M，
∵MA1与N A3平行，
∴A2B∥A1M∥A3N，
∴∠A1+∠1=180°，∠A3+∠2=180°，
又∵∠1+∠2=∠A1A2A3，
∴∠A1+∠A1A2A3+∠A3=180°+180°=360°．
故答案为：（1）180，360，540，720，1800；（2）180n度；（3）见解析.
