题目内容
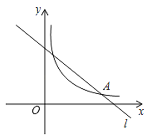
【题目】一次函数![]() 的图象是直线
的图象是直线![]() ,点A(14,1)是
,点A(14,1)是![]() 与反比例函数y=
与反比例函数y=![]() 的图象的交点.
的图象的交点.
(1)一次函数与反比例函数的表达式;
(2)将直线![]() 平移后得直线
平移后得直线![]() ,与y轴正半轴交于点B(0,t),同时交
,与y轴正半轴交于点B(0,t),同时交![]() 轴于点C,若S△ABC=18,求t的值.
轴于点C,若S△ABC=18,求t的值.
【答案】(1)一次函数表达式为![]() ,反比例函数表达式为
,反比例函数表达式为![]() =
=![]() ;
;
(2)t=3或t=12或t=![]() .
.
【解析】
(1)根据待定系数法即可求得;
(2)求得直线![]() 的解析式,得到OB=OC=t,BC=
的解析式,得到OB=OC=t,BC=![]() t,由直线
t,由直线![]() 的解析式求得E(0,15),∠DEB=45°,表示出BD,然后根据三角形的面积公式即可得到关于t的方程,解方程即可求得.
的解析式求得E(0,15),∠DEB=45°,表示出BD,然后根据三角形的面积公式即可得到关于t的方程,解方程即可求得.
(1)把点A(14,1)分别代入数![]() 和
和![]()
![]() 得,
得,
![]() ,
,![]() =
=![]() ,
,
解得![]() =15,
=15,![]() =14,
=14,
∴一次函数与反比例函数的表达式为![]() ,
,![]() =
=![]() .
.
(2)如图,由直线![]() 可知,E(0,15),∠DEB=45°,过B做BD垂直AE
可知,E(0,15),∠DEB=45°,过B做BD垂直AE
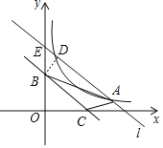
将直线![]() 平移后得直线
平移后得直线![]() ,与
,与![]() 轴正半轴交于点B(0,t),
轴正半轴交于点B(0,t),
∴直线![]() 的解析式为
的解析式为![]() ,
,
∴B(0,t),C(t,0),
∴OB=OC=t,
∴BC=![]() t,
t,
∵OE=15,OB=t,
∴BE=|15﹣t|,
①当t<15时,BD=![]() (15﹣t),
(15﹣t),
根据题意,S△ABC=![]() BC
BC![]() BD=
BD=![]() ×
×![]() (15﹣t)
(15﹣t)![]()
![]() t=18,
t=18,
解得t=3或t=12;
②当t>15时,BD=![]() (t﹣15),
(t﹣15),
根据题意,S△ABC=![]() BC
BC![]() BD=
BD=![]() ×
×![]() (t﹣15)
(t﹣15)![]()
![]() t=18,
t=18,
解得t=![]() 或t=
或t=![]() (舍去);
(舍去);
综上,若S△ABC=18,则t的值为t=3或t=12或t=![]() .
.

练习册系列答案
相关题目