Question

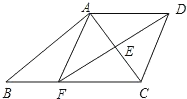
【题目】如图，已知：梯形ABCD中，AD∥BC，E为AC的中点，连接DE并延长交BC于点F，连接AF．

（1）求证：AD＝CF；

（2）在原有条件不变的情况下，请你再添加一个条件（不再增添辅助线），使四边形AFCD成为菱形，并说明理由．

Answer 1

【答案】（1）见解析；（2）添加DA＝DC，见解析

【解析】

（1）根据AD∥BC证得∠DAE＝∠FCE，∠ADE＝∠EFC，根据E为AC的中点得到AE＝CE，再利用AAS证得△DEA≌△FEC即可得到AD＝CF；

（2）若四边形AFCD成为菱形，则应证四边形AFCD是平行四边形，因而加一组邻边相等即可，如：DA＝DC．

（1）证明：在△DEA和△FEC中，

∵AD∥BC，

∴∠DAE＝∠FCE，∠ADE＝∠EFC．

又∵E为AC的中点，

∴AE＝CE．

∴△DEA≌△FEC．

∴AD＝CF．

（2）添加DA＝DC．

证明：∵AD∥BC，

又∵AD＝CF，

∴四边形AFCD为平行四边形．

又∵DA＝DC，

∴四边形AFCD为菱形．