Question

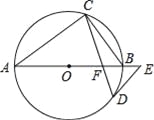
【题目】在△ABC 中，∠BAC＝90°，AD 是 BC 边上的中线，点 E 为 AD 的中点，过点 A 作 AF∥BC交 BE 的延长线于点 F，连接 CF．

（1）求证：AD＝AF；

（2）填空：①当∠ACB＝ °时，四边形 ADCF 为正方形；

②连接 DF，当∠ACB＝ °时，四边形 ABDF 为菱形．

Answer 1

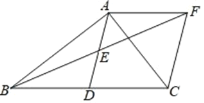
【答案】（1）见解析；（2）①45；②30

【解析】

(1)根据直角三角形的性质得到AD=CD=BD，根据全等三角形的判定和性质即可得到结论；
(2)①根据菱形的判定定理得到四边形ADCF是菱形，求得∠DCF=90°，于是得到结论；
②根据平行四边形的性质得到CD=CF，推出△DCF是等边三角形，得到DF=BD，于是得到结论．

(1)∵∠BAC=90°，AD是BC边上的中线，
∵AD=CD=BD，
∵点E为AD的中点，
∴AE=DE，
∵AF∥BC，
∴∠AFE=∠DBE，
∵∠AEF=∠DEB，
∴△AEF≌△DEB(AAS)，
∴AF=BD，
∴AD=AF；
(2)①当∠ACB=45°时，四边形ADCF为正方形；
∵AD=AF，
∴AF=CD，
∵AF∥CD，
∴四边形ADCF是菱形，
要使四边形ADCF是正方形，

则∠DCF=90°，

∴∠ACD=∠ACF=45°；
②当∠ACB=30°时，四边形ABDF为菱形；

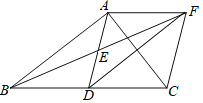
由(1)得AF=BD，AF∥BC，

∴四边形ABDF是平行四边形，
要使四边形ABDF为菱形，

∴AB=BD，
又∵AD =BD，
∴△ABD是等边三角形，
∴∠ABD=60°，
∴∠ACB=30°．
故答案为：45，30．