题目内容
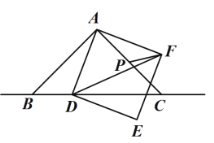
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点,点
中点,点![]() 在直线
在直线![]() 上运动,以
上运动,以![]() 为边向
为边向![]() 的右侧作正方形
的右侧作正方形![]() ,连接
,连接![]() ,则在点
,则在点![]() 的运动过程中,线段
的运动过程中,线段![]() 的最小值为:( )
的最小值为:( )
A.2B.![]() C.1D.
C.1D.![]()
【答案】B
【解析】
设Q是AB的中点,连接DQ,先证得△AQD≌△APF,得出QD=PF,根据点到直线的距离可知当QD⊥BC时,QD最小,然后根据等腰直角三角形的性质求得QD⊥BC时的QD的值,即可求得线段PF的最小值.
设Q是AB的中点,连接DQ,

∵∠BAC=∠DAF=90°,
∴∠BAC-∠DAC=∠DAF-∠DAC,即∠BAD=∠CAF,
∵AB=AC=4,P为AC中点,
∴AQ=AP,
在△AQD和△APF中,
AQ=AP
∠QAD=∠PAF,
AD=AF
∴△AQD≌△APF(SAS),
∴QD=PF,
∵点D在直线BC上运动,
∴当QD⊥BC时,QD最小,
∵△ABC是等腰直角三角形,
∴∠B=45°,
∵QD⊥BC,
∴△QBD是等腰直角三角形,
∴QD=![]()
∵QB=AB=2,
∴QD=![]() ,
,
∴线段PF的最小值是为![]() .
.
故选B.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目