题目内容
【题目】某市某工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料全部生产A,B两种产品共50件,生产A,B两种产品与所需原料情况如下表所示:
原料 型号 | 甲种原料(千克) | 乙种原料(千克) |
A产品(每件) | 9 | 3 |
B产品(每件) | 4 | 10 |
(1)该工厂生产A,B两种产品有哪几种方案?
(2)如果该工厂生产一件A产品可获利80元,生产一件B产品可获利120元,那么该工厂应该怎样安排生产可获得最大利润?
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据题意可知A、B两件产品产量总数为50件,设该工厂生产A产品x件,则生产B产品(50-x)件.根据甲、乙两种原料量和每件产品消耗原料量可列出关于x的一元一次不等式组,即可解出x的取值范围,因为x是整数,所以可得到x的所有可能取值,即可求解所有方案.(2)分别计算所有方案可获利润,并比较所获得的利润,即可求解最大利润下的生产安排.
解:(1)设工厂可安排生产x件A产品,则生产(50﹣x)件B产品
由题意得:
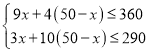 ,
,
解得:30≤x≤32的整数.
∴有三种生产方案:①A30件,B20件;②A31件,B19件;③A32件,B18件;
(2)方案(一)A,30件,B,20件时,
20×120+30×80=4800(元).
方案(二)A,31件,B,19件时,
19×120+31×80=4760(元).
方案(三)A,32件,B,18件时,
18×120+32×80=4720(元).
故方案(一)A,30件,B,20件利润最大

【题目】光明电器超市销售每台进价分别为190元、160元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 2台 | 6台 | 1840元 |
第二周 | 5台 | 7台 | 2840 元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备再采购这两种型号的电风扇共40台,这40台电风扇全部售出后,若利润不低于2660元,求A种型号的电风扇至少要采购多少台?