Question

【题目】如图，将锐角为的直角三角板MPN的一个锐角顶点P与边长为4的正方形ABCD的顶点A重合，正方形ABCD固定不动，然后将三角板绕着点A旋转，的两边分别与正方形的边BC、DC或其延长线相交于点E、F，连结EF．在三角板旋转过程中，当的一边恰好经过BC边的中点时，则EF的长为_____．

Answer 1

【答案】或

【解析】

①当MA经过BC的中点E时，延长FD至G，使DG＝BE，连接AG，先证△ABE≌△ADG，再证△GAF≌△EAF，利用勾股定理列出方程即可；②NA经过BC的中点H时，在CD上截取DQ=BE，连接AQ，同理证明△ABE≌△ADQ（SAS），再证明△QAF≌△EAF（SAS）和△ABH≌△FCH（ASA），根据勾股定理列出方程即可解决问题．

解：①当MA经过BC的中点E时，延长FD至G，使DG＝BE，连接AG，如下图所示，

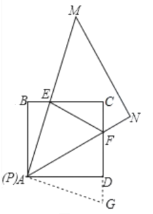
∵ABCD是正方形，
∴AB＝AD，∠ABE＝∠ADG＝∠DAB＝90°，

又∵BE=DG，
∴△ABE≌△ADG（SAS），
∴AE＝AG，∠DAG＝∠EAB，
∵∠EAF＝45°，
∴∠DAF＋∠EAB＝45°，
∴∠DAF＋∠DAG＝45°，
∴∠GAF＝∠EAF＝45°，
∵AF＝AF，
∴△GAF≌△EAF，
∴EF＝GF，
∴GF＝DF＋DG＝DF＋BE，
∴EF＝DF＋BE．

∵点E是BC的中点，

∴BE=CE=2，

设FD＝x，则FG＝EF＝2＋x，FC＝4x．
在Rt△EFC中，（x＋2）2＝（4x）2＋22，
∴x＝，
∴EF＝x＋2＝．
②当NA经过BC的中点H时，在CD上截取DQ=BE，连接AQ，如下图所示，

由情况①可知，△ABE≌△ADQ（SAS），
∴AE＝AQ，∠DAQ＝∠EAB，

∴∠DAQ+∠BAQ=∠EAB+∠BAQ=90°，
∵∠EAF＝45°，

∴∠QAF＝∠EAF＝45°，
∵AF＝AF，
∴△QAF≌△EAF（SAS），
∴EF＝QF，

又∵点H是BC的中点，

∴BH=CH，

∵∠ABH=∠FCH，∠BHA=∠CHF，

∴△ABH≌△FCH（ASA），

∴CF=AB=4，

设BE＝DQ=x，则EC＝4＋x，EF=QF＝8x，

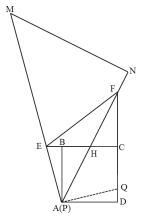
∵CH＝BH＝2，CF＝AB＝4，
由勾股定理得到：（4＋x）2＋42＝（8x）2，
∴x＝，
∴EF＝8=
综上所述，EF的长为或，

故答案为：或．