Question

【题目】如图，已知直线AC∥BD，且直线AB和AC、BD分别交于A、B两点，直线CD和AC、BD分别交于C、D两点，点P在直线AB上.

(1)如果点P在A、B两点之间运动时（如图1），试找出∠PCA、∠PDB、∠CPD之间的关系，并说出理由；

(2)如果点P在A、B两点外侧运动时（如图2，图3），问∠PCA、∠PDB、∠CPD之间的关系是否发生变化？试分别利用图2，图3探究∠PCA、∠PDB、∠CPD之间的关系（点P和A、B不重合）.

Answer 1

【答案】∠CPD=∠PCA+∠PDB，理由见解析；（2）①当点P在线段AB的延长线上运动时，∠CPD=∠PCA-∠PDB；②当点P在线段BA的延长线上运动时，∠CPD=∠PDB-∠PCA．

【解析】

（1）过点P作a的平行线，根据平行线的性质进行求解；

（2）①当点P在线段AB的延长线上运动时，过点P作b的平行线PE，由平行线的性质可得出a∥b∥PE，由此即可得出结论；②当点P在线段BA的延长线上运动时，设直线AC与DP交于点F，由三角形外角的性质可得出∠1+∠3=∠PFA，再由平行线的性质即可得出结论．

（1）如图1，过点P作PE∥a，则∠1=∠CPE．

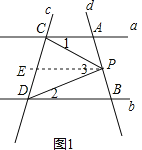
∵a∥b，PE∥a，

∴PE∥b，

∴∠2=∠DPE，

∴∠3=∠1+∠2，

即∠CPD=∠PCA+∠PDB；

（2）①当点P在线段AB的延长线上运动时，∠CPD=∠PCA-∠PDB．

理由：如图2，过点P作PE∥b，则∠2=∠EPD，

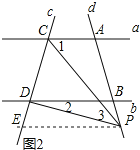
∵直线a∥b，

∴a∥PE，

∴∠1=∠EPC，

∵∠3=∠EPC-∠EPD，

∴∠3=∠1-∠2，

即∠CPD=∠PCA-∠PDB；

②当点P在线段BA的延长线上运动时，∠CPD=∠PDB-∠PCA．

证明：如图3，设直线AC与DP交于点F，

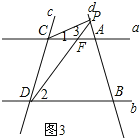
∵∠PFA是△PCF的外角，

∴∠PFA=∠1+∠3，

∵a∥b，

∴∠2=∠PFA，

∴∠2=∠1+∠3，

∴∠3=∠2-∠1，

即∠CPD=∠PDB-∠PCA．