题目内容
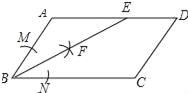
【题目】如图，四边形ABCD是平行四边形．
（1）利用尺规作∠ABC的平分线BE，交AD于E（保留作图痕迹，不写作法）；
（2）在（1）所作的图形中，求证：AB=AE．
【答案】（1）作图见解析；（2）证明见解析.
【解析】试题分析：（1）由角平分线的作法，即可得出结果；
（2）由（1）得：∠ABE=∠CBE，再由平行四边形的性质得出∠ABE=∠AEB，即可得出结论．
试题解析：（1）①以B为圆心，适当长为半径画弧，交AB于M，BC于N，
②分别以M、N为圆心，以大于
MN的长为半径画弧，两弧交于F，
③作射线BF，交AD于E，如图所示：
（2）由（1）得：∠ABE=∠CBE，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠AEB=∠CBE，
∴∠ABE=∠AEB，
∴AB=AE．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
【题目】某市某工厂现有甲种原料360千克，乙种原料290千克，计划用这两种原料全部生产A，B两种产品共50件，生产A，B两种产品与所需原料情况如下表所示：
原料 型号 | 甲种原料（千克） | 乙种原料（千克） |
A产品（每件） | 9 | 3 |
B产品（每件） | 4 | 10 |
（1）该工厂生产A，B两种产品有哪几种方案？
（2）如果该工厂生产一件A产品可获利80元，生产一件B产品可获利120元，那么该工厂应该怎样安排生产可获得最大利润？
