题目内容
【题目】在四边形![]() 中,
中,![]() .
.
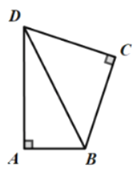
(1)如图,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长;
的长;
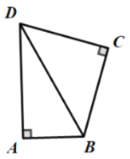
(2)如图,若![]() ,连接
,连接![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
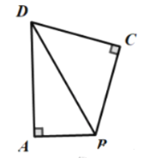
(3)在(2)的条件下,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长度为________.
的长度为________.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)先根据勾股定理求出BD,再根据勾股定理求出BC即可;
(2)连接AC,过点C作CF⊥AD于F,过点C作CE⊥AB交AB的延长线于E,可得四边形AECF是矩形,然后证明△CFD≌△CEB,求出CF=CE,可得四边形AECF是正方形,根据正方形的性质可得结论;
(3)根据全等三角形的性质和正方形的性质求出BE=1,可得正方形AECF的边长为4,然后根据勾股定理可求出AC的长度.
解:(1)∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)连接AC,过点C作CF⊥AD于F,过点C作CE⊥AB交AB的延长线于E,
则∠CFA=∠FAE=∠AEC=90°,
∴四边形AECF是矩形,
∴∠FCE=90°,
∵∠DCB=90°,
∴∠DCF=∠BCE,
又∵∠CFD=∠CEB=90°,CD=CB,
∴△CFD≌△CEB,
∴CF=CE,
∴四边形AECF是正方形,
∵AC是对角线,
∴![]() 平分
平分![]() ;
;
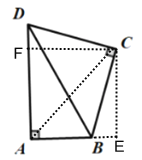
(3)由(2)可知,△CFD≌△CEB,
∴DF=BE,
∵四边形AECF是正方形,![]() ,
,![]() ,
,
∴AE=AF,即AB+BE=AD-DF,
∴3+BE=5-BE,
∴BE=1,
∴AE=4,
∴AC=![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】大成蔬菜公司以![]() 元
元![]() 千克的成本价购进
千克的成本价购进![]() 番茄,公司想知道番茄的损坏率,从所有随机抽取若干进行统计,部分结果如表:
番茄,公司想知道番茄的损坏率,从所有随机抽取若干进行统计,部分结果如表:
番茄总质量 |
|
|
|
|
|
|
损坏番茄质量 |
|
|
|
|
|
|
番茄损坏的频率 |
|
|
|
|
|
|
估计这批番茄损坏的概率为______(精确到![]() ),据此,若公司希望这批番茄能获得利润
),据此,若公司希望这批番茄能获得利润![]() 元,则销售时(去掉损坏的番茄)售价应至少定为______元/千克.
元,则销售时(去掉损坏的番茄)售价应至少定为______元/千克.
【题目】某市某工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料全部生产A,B两种产品共50件,生产A,B两种产品与所需原料情况如下表所示:
原料 型号 | 甲种原料(千克) | 乙种原料(千克) |
A产品(每件) | 9 | 3 |
B产品(每件) | 4 | 10 |
(1)该工厂生产A,B两种产品有哪几种方案?
(2)如果该工厂生产一件A产品可获利80元,生产一件B产品可获利120元,那么该工厂应该怎样安排生产可获得最大利润?