Question

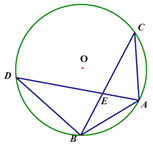
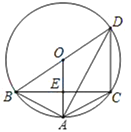
【题目】如图，△ABC内接于⊙O，∠BAC＝120°，AB＝AC，BD为⊙O的直径，CD＝6，OA交BC于点E，

求(1)∠DBC的度数；(2)弦AD的长度.

Answer 1

【答案】(1) 30；(2) .

【解析】

（1）由AB＝AC，可得，进而OA⊥BC，证明△OAB是等边三角形，由等边三角形三线合一可得∠DBC=∠OBA=30°；

（2）由直角三角形中30度角所对的边是斜边的一半可得OA=OD=6，由三角形外角的性质得∠OAD=∠ODA=30°，过O作OF⊥AD于点F，在中由勾股定理可得AF的值，进而可得AD值.

（1）∵AB＝AC，

∴，

∴OA⊥BC，

∴∠BAE＝∠CAE＝60°，BE＝EC，

∵OA＝OB，

∴△OAB是等边三角形，

∴∠OBA=60°，

∵BE⊥OA，

∴∠DBC=∠OBA=30°；

（2）∵BD为⊙O的直径，CD＝6，∠DBC =30°，

BD=2CD=12，OA=OD=6，

∴∠OAD=∠ODA，

∵∠OAD+∠ODA=∠AOB=60°，

∴∠OAD=∠ODA=30°，

过O作OF⊥AD于点F，则AF=DF，

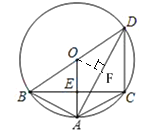
在中，OA=6，∠OAF=30°，

∴OF=3，

∴=,

∴AD=2AF=