Question

【题目】如图，己知直线过与交于点、点，与交于点，直线与轴交于点，且，则________．

Answer 1

【答案】10

【解析】

过点A作AE⊥x轴于E，过点B作BG⊥x轴于G，先利用待定系数法求得函数的解析式，再根据，求得BG=2，从而求得B点坐标，然后用待定系数法求得一次函数的解析式，再求得C点坐标，根据对称点的性质求得E点坐标，最后求得k的值即可.

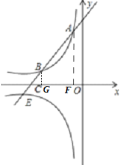过点A作AE⊥x轴于E，过点B作BG⊥x轴于G，易得△BCG∽△ACO，

将A坐标代入反比例函数，得m=﹣6，

即反比例函数的解析式为，

∵A（﹣1，6），

∴AF=6，OF=1，

∵，

∴，

∴BG=AF=2，

把y=2代入，

解得：x=﹣3，即B（﹣3，2），

将A，B坐标代入直线中得，

，

解得：a=2，b=8，

∴直线AB的解析式为y=2x+8，

令y=0，得到x=﹣4，即C（﹣4，0），

∵BE=2BC，

∴C为BE中点，

∴E（﹣5，﹣2），

将E坐标代入，得：k=10.

故答案为：10.