题目内容
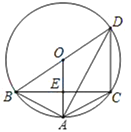
【题目】如图，⊙O是△ABC的外接圆，AB=AC，D是优弧BC上的一个动点，连结AD交BC于点E，连结BD.
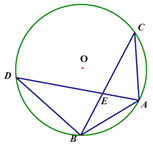
（1）若AE=2，DE=8，求AC的长;
（2）若D是优弧BC上中点时，求证：
.
【答案】（1）
（2）详见解析.
【解析】
（1）根据AB=AC推出∠BAE=∠BAD，然后根据同弧推出∠BDA=∠BCA，则ABE~ABD，即可推出
，即可求解AB；
（2）根据D是优弧BC上中点，推出
,通过AB=AC推出AD为⊙O的直径，然后证明ACE~CDE, 推出
，又CE=
BC，即可证明
.
解：（1）∵AB=AC
∴∠BAE=∠BAD
∵根据同弧
∴推出∠BDA=∠BCA
∴ABE~ABD
∴
∵AE=2，DE=8
∴
（2）如图
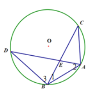
∵D是优弧BC上中点
∴
∴CD=BD
∵AB=AC
∴AD垂直平分BC
∴AD为⊙O的直径
∴∠ACD=∠CED=90°，∠1+∠2=∠1+∠3=90°
∴∠2=∠3
∴ACE~CDE
∴
∴
又CE=BC
∴
∴
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
