题目内容
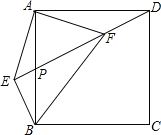
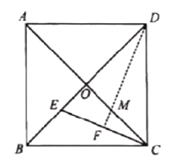
【题目】如图,边长为![]() 的正方形
的正方形![]() 的对角线
的对角线![]() 与
与![]() 交于点
交于点![]() ,将正方形
,将正方形![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() ,则
,则![]()
![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
过点M作MP⊥CD垂足为P,过点O作OQ⊥CD垂足为Q,根据正方形的性质得到AB=AD=BC=CD=![]() ,∠DCB=∠COD=∠BOC=90°,根据折叠的性质得到∠EDF=∠CDF,设OM=PM=x,根据相似三角形的性质即可得到结论.
,∠DCB=∠COD=∠BOC=90°,根据折叠的性质得到∠EDF=∠CDF,设OM=PM=x,根据相似三角形的性质即可得到结论.
过点M作MP⊥CD垂足为P,过点O作OQ⊥CD垂足为Q,
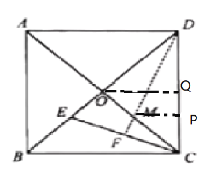
∵ 正方形的边长为![]() ,
,
∴OD=1, OC=1, OQ=DQ=![]() ,由折叠可知,∠EDF=∠CDF.
,由折叠可知,∠EDF=∠CDF.
又∵AC⊥BD, ∴OM=PM,
设OM=PM=x
∵OQ⊥CD,MP⊥CD
∴∠OQC=∠MPC=900, ∠PCM=∠QCO,
∴△CMP∽△COQ
∴![]() , 即
, 即 , 解得x=
, 解得x=![]() -1
-1
∴OM=PM=![]() -1.
-1.
故选D

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目