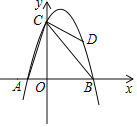题目内容
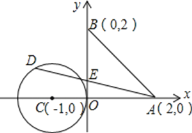
【题目】如图,已知A,B两点的坐标分别为(2,0),(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E ,则△ABE面积的最小值是 _____
【答案】![]()
【解析】
根据三角形的面积公式,△ABE底边BE上的高AO不变,BE越小,则面积越小,可以判断当AD与⊙C相切时,BE的值最小,根据勾股定理求出AD的值,然后根据相似三角形对应边成比例列式求出OE的长度,代入三角形的面积公式进行计算即可求解.
解:如图所示,当AD与⊙C相切时,BE最短,此时△ABE面积最小,
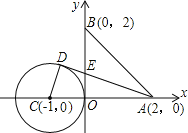
∵A(2,0),C(-1,0),⊙C半径为1,
∴AO=2,AC=2+1=3,CD=1,
在Rt△ACD中,AD=![]() ,
,
∵CD⊥AD,
∴∠D=90°,
∴∠D=∠AOE,
在△AOE与△ADC中,![]() ,
,
∴△AOE∽△ADC,
∴![]()
即![]() ,
,
解得EO=![]() ,
,
∵点B(0,2),
∴OB=2,
∴BE=OB-OE=2-![]() ,
,
∴△ABE面积的最小值=![]() ×BE×AO=
×BE×AO=![]() (2-
(2-![]() )×2=2-
)×2=2-![]() .
.
故答案为:2-![]() .
.

练习册系列答案
相关题目