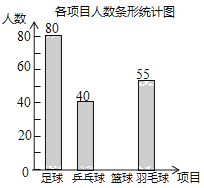
题目内容
【题目】阅读与理解:
三角形中一边中点与这边所对顶点的线段称为三角形的中线。
三角形的中线的性质:三角形的中线等分三角形的面积。
即如图1,AD是![]() 中BC边上的中线,则
中BC边上的中线,则![]() ,
,
理由:![]() ,
,![]() ,
,
即:等底同高的三角形面积相等。
操作与探索:

在如图2至图4中,![]() 的面积为a。
的面积为a。
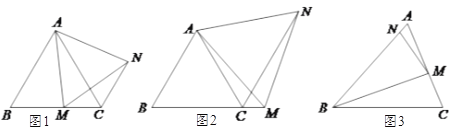
(1)如图2,延长![]() 的边BC到点D,使CD=BC,连接DA,若
的边BC到点D,使CD=BC,连接DA,若![]() 的面积为
的面积为![]() ,则
,则![]() (用含a的代数式表示);
(用含a的代数式表示);
(2)如图3,延长![]() 的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若
的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若![]() 的面积为
的面积为![]() ,则
,则![]() _________(用含a的代数式表示);
_________(用含a的代数式表示);
(3)在图3的基础上延长AB到点F,使BF=AB,连接FD,FE,得到![]() (如图4),若阴影部分的面积为
(如图4),若阴影部分的面积为![]() ,则
,则![]() ________(用含a的代数式表示)
________(用含a的代数式表示)
(4)拓展与应用:
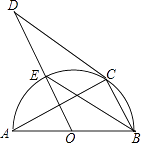
如图5,已知四边形ABCD的面积是a;E,F,G,H分别是AB,BC,CD的中点,求图中阴影部分的面积?

【答案】(1)a;(2)2a;(3)6a;(4)0.5a.
【解析】
(1)根据阅读材料中所得结论易得S1=a;
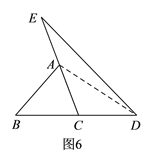
(2)如图6,连接AD,由阅读材料中中所得结论结合已知条件易得S△ADE=S△ACD=S△ABC=a,由此可得S2=2a;
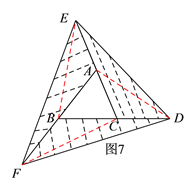
(3)如图7,连接AD、BE、CF,由(2)中结论可得S△CDE=2a,S△AEF=2a,S△BDF=2a,然后由S3= S△CDE+S△AEF+S△BDF即可求得S3=6a;
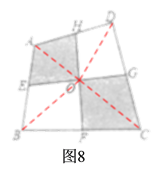
(4)如图8,连接OA、OB、OC、OD,则由阅读材料中的结论可得:S△AOE=![]() S△AOB,S△AOH=
S△AOB,S△AOH=![]() S△AOD,S△COF=
S△AOD,S△COF=![]() S△BOC,S△COG=
S△BOC,S△COG=![]() S△COD,将上述等式相交即可得到S阴影=
S△COD,将上述等式相交即可得到S阴影=![]() S四边形ABCD=
S四边形ABCD=![]() .
.
(1)如图2,由题意可得:在△ABD中,AC是BD边上的中线,
∴S1=S△ACD=S△ABC=a;
(2)如图6,连接AD,则由题意可知,AD是△CDE的边CE上的中线,
∴S△ADE=S△ACD,
又∵S△ACD=S△ABC=a ,
∴S2= S△ADE+S△ACD=2a;
(3)如图7,连接AD、BE和CF,则由(2)中结论可得:
S△CDE=2a,S△AEF=2a,S△BDF=2a,
∵S3= S△CDE+S△AEF+S△BDF,
∴S3=2a+2a+2a=6a;
(4)如图8,连接连接OA、OB、OC、OD,
∵点E、F、G、H分别是四边形ABCD四边的中点,
∴S△AOE=![]() S△AOB,S△AOH=
S△AOB,S△AOH=![]() S△AOD,S△COF=
S△AOD,S△COF=![]() S△BOC,S△COG=
S△BOC,S△COG=![]() S△COD,
S△COD,
∴S阴影=S△AOE+S△AOH+S△COF+S△COG
=![]() S△AOB+
S△AOB+![]() S△AOD+
S△AOD+![]() S△BOC+
S△BOC+![]() S△COD
S△COD
=![]() S四边形ABCD
S四边形ABCD
=![]() .
.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案