题目内容
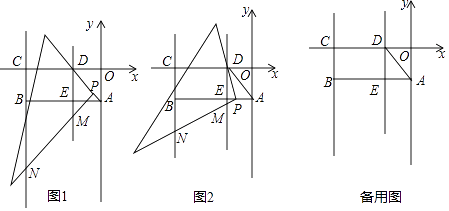
【题目】如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC. 
(1)试判断△ABC的形状,并说明理由;
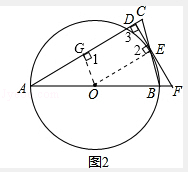
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2﹣ ![]() ,求⊙O的半径和BF的长.
,求⊙O的半径和BF的长.
【答案】
(1)解:△ABC是等腰三角形,理由是:
如图1,连接OE,
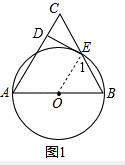
∵DE是⊙O的切线,
∴OE⊥DE,
∵ED⊥AC,
∴AC∥OE,
∴∠1=∠C,
∵OB=OE,
∴∠1=∠B,
∴∠B=∠C,
∴△ABC是等腰三角形;
(2)解:如图2,过点O作OG⊥AC,垂足为G,则得四边形OGDE是矩形,
∵△ABC是等腰三角形,
∴∠B=∠C=75°,
∴∠A=180°﹣75°﹣75°=30°,
设OG=x,则OA=OB=OE=2x,AG= ![]() x,
x,
∴DG=OE=2x,
根据AC=AB得:4x= ![]() x+2x+2﹣
x+2x+2﹣ ![]() ,
,
x=1,
∴OE=OB=2,
在直角△OEF中,∠EOF=∠A=30°,
cos30= ![]() ,OF=
,OF= ![]() =2÷
=2÷ ![]() =
= ![]() ,
,
∴BF= ![]() ﹣2,⊙O的半径为2.
﹣2,⊙O的半径为2.
【解析】(1)连接OE,根据切线性质得OE⊥DE,与已知中的ED⊥AC得平行,由此得∠1=∠C,再根据同圆的半径相等得∠1=∠B,可得出三角形为等腰三角形;(2)通过作辅助线构建矩形OGDE,再设与半径有关系的边OG=x,通过AB=AC列等量关系式,可求得结论.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目