题目内容
【题目】如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( ) 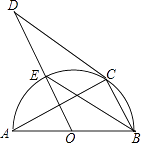
A.AC⊥BC
B.BE平分∠ABC
C.BE∥CD
D.∠D=∠A
【答案】C
【解析】解:连接OC. ∵AB是直径,
∴∠ACB=90°,
∴AC⊥BC,故A正确,
∵OD∥BC,
∴∠EBC=∠BEO,
∵OE=OB,
∴∠OEB=∠OBE,
∴∠EBO=∠EBC,
∴BE平分∠ABC,故B正确,
∵DC是切线,
∴DC⊥CO,
∴∠DCO=90°,
∴∠D+∠DOC=90°,
∵BC⊥AC,OD∥BC,
∴OD⊥AC,
∵OA=OC,
∴∠AOD=∠DOC,
∴∠A+∠AOD=90°,
∴∠A=∠D,故D正确.
无法判断C正确,
故选C.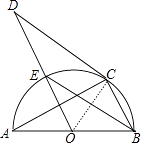
【考点精析】关于本题考查的切线的性质定理,需要了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
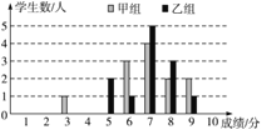
【题目】(8分)一次学科测验,学生得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分为优秀.这次测验中甲、乙两组学生成绩分布的条形统计图如图.
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
甲组 | 6.9 | 2.4 | 91.7% | 16.7% | |
乙组 | 1.3 | 83.3% | 8.3% |
(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要高于甲组.请你给出三条支持乙组学生观点的理由.