题目内容
【题目】已知:直线AB∥CD,点E,F分别在直线AB,CD上,点M为平面内一点.
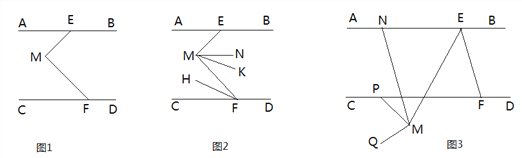
(1)如图1,∠AEM,∠M,∠CFM的数量关系为 ;(直接写出答案)
(2)如图2,∠AEM=48°,MN平分∠EMF,FH平分∠MFC,MK∥FH,求∠NMK的度数;
(3)如图3,点P为CD上一点,∠BEF=n·∠MEF,∠PMQ=n·∠PME,过点M作MN∥EF交AB于点N,请直接写出∠PMQ,∠BEF,∠PMN之间的数量关系.(用含n的式子表示)
【答案】(1)∠M=∠AEM+∠CFM(2)24° (3)n∠PMN=∠PMQ-∠BEF
【解析】
(1)如图1,过点M作ML∥AB,
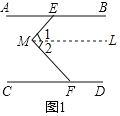
∵AB∥CD,
∴ML∥AB∥CD,
∴∠1=∠AEM,∠2=∠CFM,
∵∠EMF=∠1+∠2,
∴∠M=∠AEM+∠CFM;
(2)∵MN平分∠EMF,FH平分∠MFC,
∴![]()
∵MK∥FH,
∴![]()
∵∠EMF=∠AEM+∠MFC,
∴![]()
∴![]()
(3)
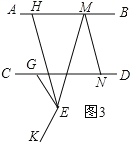
n∠PMN=∠PMQ∠BEF.
∵∠BEF=n∠MEF,∠PMQ=n∠PME,
∴![]()
∵MN∥EF,
∴![]()
∵![]()
∴n∠PMN=∠PMQ∠BEF.

练习册系列答案
相关题目