题目内容
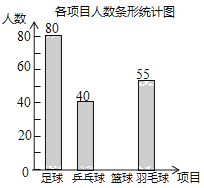
【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于 度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是 人。

【答案】(1)250;(2)条形图见解析;(3)108;(4)480.
【解析】试题分析:(1)由喜欢足球的人数除以所占的百分比即可求出总人数;
(2)由总人数减去喜欢足球、乒乓球、羽毛球的人数,即可求出喜欢篮球C的人数,补全统计图即可;(3)用360乘以选择篮球项目的人数所占的百分比即可;(4)用1500乘以喜欢足球的人数所占的百分比即可得该学校选择足球项目的学生人数.
试题解析:
(1) 根据题意得:80÷32%=250(人),
则这次被调查的学生共有250人;
(2)喜欢篮球的人数为:250-80-75-55=40(人),补全统计图如下:

(3)360×![]() =108°.
=108°.
(4)1500×32%=480(人)
∴该学校选择足球项目的学生人数约是480人.

【题目】希望中学八年级学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩较好的甲班和乙班5名学生的比赛成绩(单位:个)
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)求两班比赛数据的中位数;
(2)计算两班比赛数据的方差,并比较哪一个小;
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.
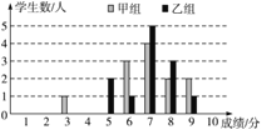
【题目】(8分)一次学科测验,学生得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分为优秀.这次测验中甲、乙两组学生成绩分布的条形统计图如图.
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
甲组 | 6.9 | 2.4 | 91.7% | 16.7% | |
乙组 | 1.3 | 83.3% | 8.3% |
(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要高于甲组.请你给出三条支持乙组学生观点的理由.